8 Analiza dyskryminacyjna

Analiza dyskryminacyjna (ang. discriminant analysis) jest grupą technik dyskryminacji obserwacji względem przynależności do klas. Część z nich należy do klasyfikatorów liniowych (choć nie zawsze w ścisłym sensie). Za autorów tej metody uważa się Fisher’a -Fisher (1936) i Welch’a -Welch (1939). Każdy z nich prezentował nieco inne podejście do tematu klasyfikacji. Welch poszukiwał klasyfikacji minimalizującej prawdopodobieństwo błędnej klasyfikacji, znane jako klasyfikatory bayesowskie. Podejście Fisher’a skupiało się raczej na porównaniu zmienności międzygrupowej do zmienności wewnątrzgrupowej. Wychodząc z założenia, że iloraz tych wariancji powinien być stosunkowo duży przy różnych klasach, jeśli do ich opisu użyjemy odpowiednich zmiennych niezależnych. W istocie chodzi o znalezienie takiego wektora, w kierunku którego wspomniany iloraz wariancji jest największy.

8.1 Liniowa analiza dyskryminacyjna Fisher’a

8.1.1 Dwie kategorie zmiennej grupującej

Niech \(\boldsymbol D\) będzie zbiorem zawierającym \(n\) punktów \(\{\boldsymbol x, y\}\), gdzie \(\boldsymbol x\in \mathbb{R}^d\), a \(y\in \{c_1,\ldots,c_k\}\). Niech \(\boldsymbol D_i\) oznacza podzbiór punktów zbioru \(\boldsymbol D\), które należą do klasy \(c_i\), czyli \(\boldsymbol D_i=\{\boldsymbol x|y=c_i\}\) i niech \(|\boldsymbol D_i|=n_i\). Na początek załóżmy, że \(\boldsymbol D\) składa się tylko z \(\boldsymbol D_1\) i \(\boldsymbol D_2\).

Niech \(\boldsymbol w\) będzie wektorem jednostkowym (\(\boldsymbol w'\boldsymbol w=1\)), wówczas rzut ortogonalny punku \(\boldsymbol x_i\) na wektor \(\boldsymbol w\) można zapisać następująco \[\begin{equation} \tilde{\boldsymbol x}=\left(\frac{\boldsymbol w'\boldsymbol x}{\boldsymbol w'\boldsymbol w}\right)\boldsymbol w=(\boldsymbol w'\boldsymbol x)\boldsymbol w = a\boldsymbol w, \end{equation}\] gdzie \(a\) jest współrzędną punktu \(\tilde{\boldsymbol x}\) w kierunku wektora \(\boldsymbol w\), czyli \[\begin{equation} a=\boldsymbol w'\boldsymbol x. \end{equation}\] Zatem \((a_1,\ldots,a_n)\) reprezentują odwzorowanie \(\mathbb{R}^d\) w \(\mathbb{R}\), czyli z \(d\)-wymiarowej przestrzeni w przestrzeń generowaną przez \(\boldsymbol w\).

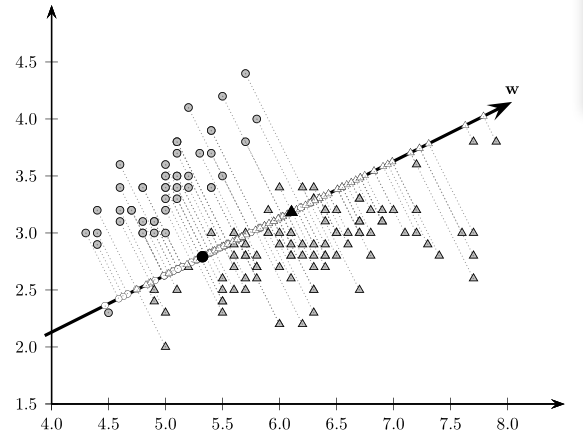
Rysunek 8.1: Rzut ortogonalny punktów w kierunku wektora \(\boldsymbol w\)

Każdy punkt należy do pewnej klasy, dlatego możemy wyliczyć \[\begin{align} m_1=&\frac{1}{n_1}\sum_{ \boldsymbol x\in \boldsymbol D_1}a=\\ =&\frac{1}{n_1}\sum_{ \boldsymbol x\in \boldsymbol D_1} \boldsymbol w' \boldsymbol x=\\ =& \boldsymbol w'\left(\frac{1}{n_1}\sum_{ \boldsymbol x\in \boldsymbol D_1} \boldsymbol x \right)=\\ =& \boldsymbol w' \boldsymbol{\mu}_1, \tag{8.1} \end{align}\] gdzie \(\boldsymbol \mu_1\) jest wektorem średnich punktów z \(\boldsymbol D_1\). W podobny sposób można policzyć \(m_2 = \boldsymbol w' \boldsymbol \mu_2\). Oznacza to, że średnia projekcji jest projekcją średnich.

Rozsądnym wydaje się teraz poszukać takiego wektora, aby \(|m_1-m_2|\) była maksymalnie duża przy zachowaniu niezbyt dużej zmienności wewnątrz grup. Dlatego kryterium Fisher’a przyjmuje postać \[\begin{equation} \max_{ \boldsymbol w}J(\boldsymbol w)=\frac{(m_1-m_2)^2}{ss_1^2+ss_2^2}, \tag{8.2} \end{equation}\] gdzie \(ss_j^2=\sum_{ \boldsymbol x\in \boldsymbol D_j}(a-m_j)^2=n_j\sigma_j^2.\)

Zauważmy, że licznik w (8.2) da się zapisać jako \[\begin{align} (m_1-m_2)^2=& ( \boldsymbol w'( \boldsymbol \mu_1- \boldsymbol \mu_2))^2=\\ =& \boldsymbol w'(\boldsymbol \mu_1- \boldsymbol \mu_2)(\boldsymbol \mu_1- \boldsymbol \mu_2)'\boldsymbol w=\\ =& \boldsymbol w' \boldsymbol B \boldsymbol w \end{align}\] gdzie \(\boldsymbol B=(\boldsymbol \mu_1- \boldsymbol \mu_2)(\boldsymbol \mu_1- \boldsymbol \mu_2)'\) jest macierzą \(d\times d\).

Ponadto \[\begin{align} ss_j^2=&\sum_{ \boldsymbol x\in \boldsymbol D_j}(a-m_j)^2=\\ =&\sum_{ \boldsymbol x\in \boldsymbol D_j}( \boldsymbol w' \boldsymbol x- \boldsymbol w' \boldsymbol\mu_j)^2=\\ =& \sum_{ \boldsymbol x\in \boldsymbol D_j}( \boldsymbol{w}'( \boldsymbol{x}- \boldsymbol{\mu}_j))^2=\\ =& \boldsymbol{w}'\left(\sum_{ \boldsymbol x\in \boldsymbol D_j}(\boldsymbol{x}-\boldsymbol \mu_j)(\boldsymbol x- \boldsymbol \mu_j)'\right) \boldsymbol{w}=\\ =& \boldsymbol{w}' \boldsymbol{S}_j \boldsymbol{w}, \tag{8.3} \end{align}\] gdzie \(\boldsymbol{S}_j=n_j \boldsymbol{\Sigma}_j\). Zatem mianownik (8.2) możemy zapisać jako \[\begin{equation} ss_1^2+ss_2^2= \boldsymbol{w}'(\boldsymbol{S}_1+ \boldsymbol{S}_2) \boldsymbol{w}= \boldsymbol{w}' \boldsymbol{S} \boldsymbol{w}, \end{equation}\] gdzie \(\boldsymbol{S}=\boldsymbol{S}_1+\boldsymbol{S}_2\). Ostatecznie warunek Fisher’a przyjmuje postać \[\begin{equation} \max_{ \boldsymbol{w}}J( \boldsymbol{w})=\frac{ \boldsymbol{w}' \boldsymbol{B} \boldsymbol{w}}{ \boldsymbol{w}' \boldsymbol{S} \boldsymbol{w}}. \tag{8.4} \end{equation}\]

Różniczkując (8.4) po \(\boldsymbol{w}\) i przyrównując go do 0, otrzymamy warunek \[\begin{equation} \boldsymbol{B} \boldsymbol{w} = \lambda \boldsymbol{S} \boldsymbol{w}, \tag{8.5} \end{equation}\] gdzie \(\lambda=J(\boldsymbol{w})\). Maksimum (8.4) jest osiągane dla wektora \(\boldsymbol{w}\) równego wektorowi własnemu odpowiadającemu największej wartości własnej równania charakterystycznego \(|\boldsymbol{B}-\lambda\boldsymbol{S}|=0\). Jeśli \(\boldsymbol{S}\) nie jest osobliwa, to rozwiązanie (8.5) otrzymujemy przez znalezienie największej wartości własnej macierzy \(\boldsymbol{B}\boldsymbol{S}^{-1}\) lub bez wykorzystania wartości i wektorów własnych.

Ponieważ \(\boldsymbol{B}\boldsymbol w=\left((\boldsymbol{\mu}_1-\boldsymbol{\mu}_2)(\boldsymbol{\mu}_1-\boldsymbol{\mu}_2)'\right)\boldsymbol{w}\) jest macierzą \(d \times 1\) rzędu 1, to \(\boldsymbol{B}\boldsymbol{w}\) jest punktem na kierunku wyznaczonym przez wektor \(\boldsymbol{\mu}_1-\boldsymbol{\mu}_2\), bo \[\begin{align} \boldsymbol{B}\boldsymbol{w}=& \left((\boldsymbol{\mu}_1-\boldsymbol{\mu}_2)(\boldsymbol{\mu}_1-\boldsymbol{\mu}_2)'\right)\boldsymbol{w}=\\ =&(\boldsymbol{\mu}_1-\boldsymbol{\mu}_2)((\boldsymbol{\mu}_1-\boldsymbol{\mu}_2)'\boldsymbol{w})=\\ =& b(\boldsymbol{\mu}_1-\boldsymbol{\mu}_2), \end{align}\] gdzie \(b = (\boldsymbol{\mu}_1-\boldsymbol{\mu}_2)'\boldsymbol{w}\) jest skalarem.

Wówczas (8.5) zapiszemy jako \[\begin{gather} b(\boldsymbol{\mu}_1-\boldsymbol{\mu}_2) = \lambda\boldsymbol{S}\boldsymbol{w}\\ \boldsymbol{w}= \frac{b}{\lambda}\boldsymbol{S}^{-1}(\boldsymbol{\mu}_1-\boldsymbol{\mu}_2) \end{gather}\]

A ponieważ \(b/\lambda\) jest liczbą, to kierunek najlepszej dyskryminacji grup wyznacza wektor \[\begin{equation} \boldsymbol{w}=\boldsymbol{S}^{-1}(\boldsymbol{\mu}_1-\boldsymbol{\mu}_2). \end{equation}\]

Rysunek 8.2: Rzut ortogonalny w kierunku wektora \(\boldsymbol{w}\), będącego najlepiej dyskryminującym obie grupy obserwacji

8.1.2 \(k\)-kategorii zmiennej grupującej

Uogólnieniem tej teorii na przypadek \(k\) klas otrzymujemy przez uwzględnienie \(k-1\) funkcji dyskryminacyjnych. Zmienność wewnątrzgrupowa przyjmuje wówczas postać \[\begin{equation} \boldsymbol{S}_W=\sum_{i=1}^k\boldsymbol{S}_i, \end{equation}\] gdzie \(\boldsymbol{S}_i\) jest zdefiniowane jak w (8.3). Niech średnia i zmienność całkowita będą dane wzorami \[\begin{equation} \boldsymbol{m}=\frac{1}{n}\sum_{i=1}^kn_i\boldsymbol{m}_i, \end{equation}\] \[\begin{equation} \boldsymbol{S}_T=\sum_{j=1}^k\sum_{\boldsymbol{x}\in D_j}(\boldsymbol{x}-\boldsymbol{m})(\boldsymbol{x}-\boldsymbol{m})' \end{equation}\] gdzie \(\boldsymbol{m}_i\) jest określone jak w (8.1). Wtedy zmienność międzygrupową możemy wyrazić jako \[\begin{equation} \boldsymbol{S}_B=\sum_{i=1}^kn_i(\boldsymbol{m}_i-\boldsymbol{m})(\boldsymbol{m}_i-\boldsymbol{m})', \end{equation}\] bo \(\boldsymbol{S}_T=\boldsymbol{S}_W+\boldsymbol{S}_B.\) Określamy projekcję \(d\)-wymiarowej przestrzeni na \(k-1\)-wymiarową przestrzeń za pomocą \(k-1\) funkcji dyskryminacyjnych postaci \[\begin{equation} a_j=\boldsymbol{w}_j'\boldsymbol{x}, \quad j=1,\ldots,k-1. \end{equation}\] Połączone wszystkie \(k-1\) rzutów możemy zapisać jako \[\begin{equation} \boldsymbol{a}=\boldsymbol{W}'\boldsymbol{x}. \end{equation}\]

W nowej przestrzeni \(k-1\)-wymiarowej możemy zdefiniować \[\begin{equation} \tilde{\boldsymbol{m}}=\frac{1}{n}\sum_{i=1}^kn_i\tilde{\boldsymbol{m}}_i, \end{equation}\] gdzie \(\tilde{\boldsymbol{m}}_i= \frac{1}{n_i}\sum_{\boldsymbol{a}\in A_i}\boldsymbol{a}\), a \(A_i\) jest projekcją obiektów z \(i\)-tej klasy na hiperpowierzchnię generowaną przez \(\boldsymbol{W}\). Dalej możemy zdefiniować zmienności miedzy- i wewnątrzgrupowe dla obiektów przekształconych przez \(\boldsymbol{W}\) \[\begin{align} \tilde{\boldsymbol{S}}_W=&\sum_{i=1}^k\sum_{\boldsymbol{a}\in A_i}(\boldsymbol{a}-\tilde{\boldsymbol{m}})(\boldsymbol{a}-\tilde{\boldsymbol{m}})'\\ \tilde{\boldsymbol{S}}_B=&\sum_{i=1}^kn_i(\tilde{\boldsymbol{m}}_i-\tilde{\boldsymbol{m}})(\tilde{\boldsymbol{m}}_i-\tilde{\boldsymbol{m}})'. \end{align}\] Łatwo można zatem pokazać, że \[\begin{align} \tilde{\boldsymbol{S}}_W = & \boldsymbol{W}'\boldsymbol{S}_W\boldsymbol{W}\\ \tilde{\boldsymbol{S}}_B = & \boldsymbol{W}'\boldsymbol{S}_B\boldsymbol{W}. \end{align}\] Ostatecznie warunek (8.2) w \(k\)-wymiarowym ujęciu można przedstawić jako \[\begin{equation} \max_{\boldsymbol{W}}J(\boldsymbol{W})=\frac{\tilde{\boldsymbol{S}}_B}{\tilde{\boldsymbol{S}}_W}=\frac{\boldsymbol{W}'\boldsymbol{S}_B\boldsymbol{W}}{\boldsymbol{W}'\boldsymbol{S}_W\boldsymbol{W}}. \end{equation}\] Maksimum można znaleźć poprzez rozwiązanie równania charakterystycznego \[\begin{equation} |\boldsymbol{S}_B-\lambda_i\boldsymbol{S}_W|=0 \end{equation}\] dla każdego \(i\).

Przykład 8.1 Dla danych ze zbioru iris przeprowadzimy analizę dyskryminacji. Implementację metody LDA znajdziemy w pakiecie MASS w postaci funkcji lda.

Zaczynamy od standaryzacji zmiennych i podziału próby na uczącą i testową.

library(MASS)
library(tidyverse)
iris.std <- iris %>% 
    mutate_if(is.numeric, scale)
set.seed(44)
ind <- sample(nrow(iris.std), size = 100)
dt.ucz <- iris.std[ind,]
dt.test <- iris.std[-ind,]

Budowa modelu

mod.lda <- lda(Species~., data = dt.ucz)
mod.lda$prior

##     setosa versicolor  virginica 
##       0.32       0.32       0.36

Prawdopodobieństwa a priori przynależności do klas przyjęto na podstawie próby uczącej.

mod.lda$means

##            Sepal.Length Sepal.Width Petal.Length Petal.Width
## setosa      -1.05240186   0.7790042   -1.2968064  -1.2536554
## versicolor   0.04201557  -0.6764307    0.2521529   0.1607657
## virginica    0.87352122  -0.2398799    1.0182730   1.0868584

W części means wyświetlone są średnie poszczególnych zmiennych niezależnych w podziale na grupy. Dzięki temu można określić położenia środków ciężkości poszczególnych klas w oryginalnej przestrzeni.

mod.lda$scaling

##                     LD1         LD2
## Sepal.Length  0.5884101  0.04738098
## Sepal.Width   0.7566030 -0.97757574
## Petal.Length -3.2910346  1.41170784
## Petal.Width  -2.3799488 -1.95325155

Powyższa tabela zawiera współrzędne wektorów wyznaczających funkcje dyskryminacyjne. Na ich podstawie możemy określić, która z nich wpływa najmocniej na tworzenie się nowej przestrzeni.

Obiekt svd przechowuje pierwiastki z \(\lambda_i\), dlatego podnosząc je do kwadratu i dzieląc przez ich sumę otrzymamy udział poszczególnych zmiennych w dyskryminacji przypadków. Jak widać pierwsza funkcja dyskryminacyjna w zupełności by wystarczyła.

mod.lda$svd^2/sum(mod.lda$svd^2)

## [1] 0.992052359 0.007947641

Klasyfikacja na podstawie modelu

pred.lda <- predict(mod.lda, dt.test)

Wynik predykcji przechowuje trzy rodzaje obiektów:

• klasy, które przypisał obiektom model (class);
• prawdopodobieństwa a posteriori przynależności do klas na podstawie modelu (posterior);
• współrzędne w nowej przestrzeni LD1, LD2 (x).

Sprawdzenie jakości klasyfikacji

tab <- table(pred = pred.lda$class, obs = dt.test$Species)
tab

##             obs
## pred         setosa versicolor virginica
##   setosa         18          0         0
##   versicolor      0         17         1
##   virginica       0          1        13

sum(diag(prop.table(tab)))

## [1] 0.96

Jak widać z powyższej tabeli model dobrze sobie radzi z klasyfikacją obiektów. Odsetek poprawnych klasyfikacji wynosi 96%.

cbind.data.frame(obs = dt.test$Species,
                 pred.lda$x, 
                 pred = pred.lda$class) %>% 
    ggplot(aes(x = LD1, y = LD2))+
    geom_point(aes(color = pred, shape = obs), size = 2)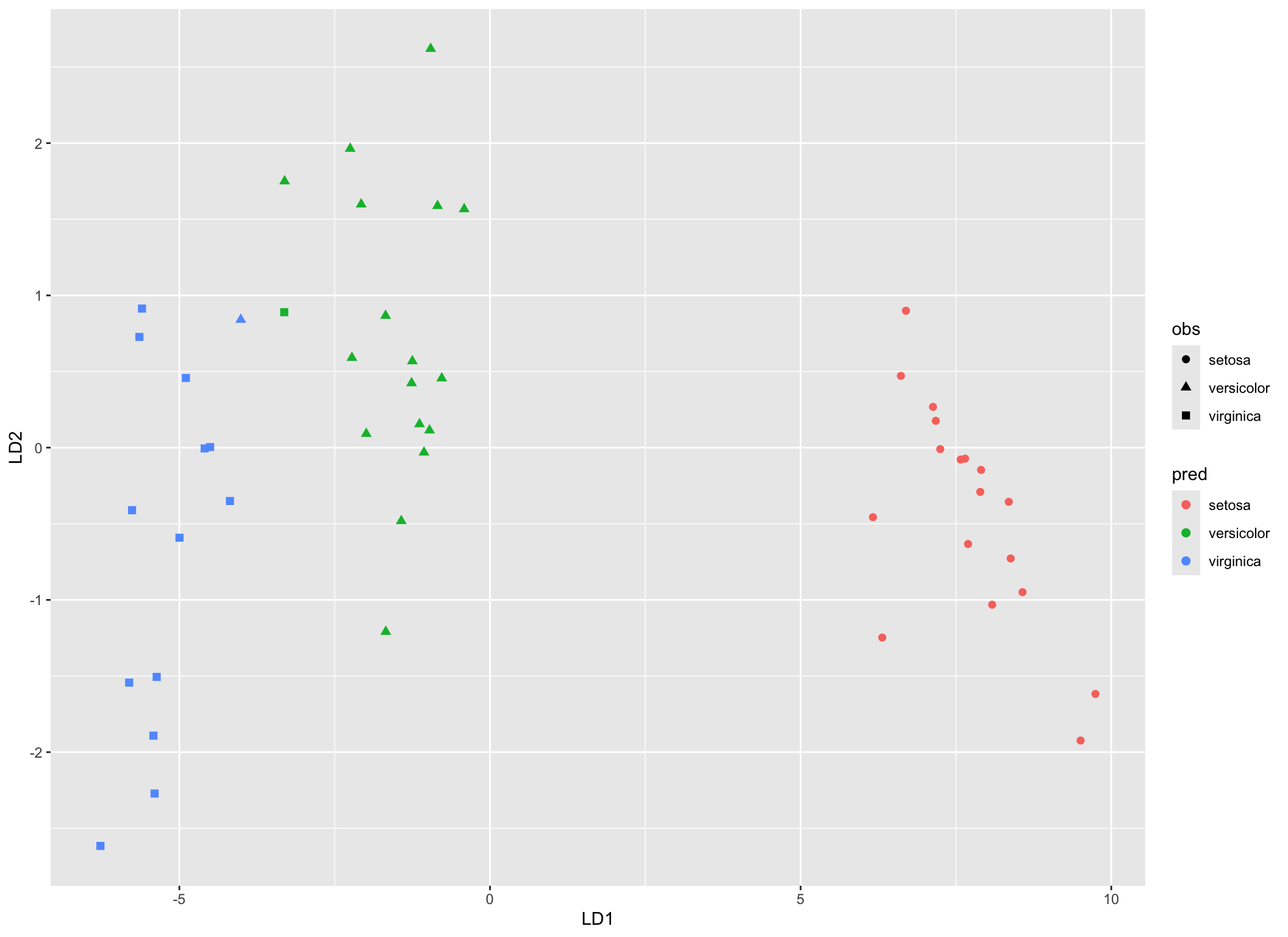

Rysunek 8.3: Klasyfikacja w przestrzeni LD1, LD2 na podstawie modelu mod.lda

8.2 Liniowa analiza dyskryminacyjna - podejście probabilistyczne

Jak wspomniano na wstępie (patrz rozdział 8), podejście prezentowane przez Welcha polegało na minimalizacji prawdopodobieństwa popełnienia błędu przy klasyfikacji. Cała rodzina klasyfikatorów Bayesa (patrz rozdział 9) polega na wyznaczeniu prawdopodobieństw a posteriori, na podstawie których dokonuje się decyzji o klasyfikacji obiektów. Tym razem dodajemy również założenie, że zmienne niezależne \(\boldsymbol{x}=(\boldsymbol{x}_1,\ldots,\boldsymbol{x}_d)\) charakteryzują się wielowymiarowym rozkładem normalnym \[\begin{equation} f(\boldsymbol{x}) = \frac{1}{(2\pi)^{d/2}|\boldsymbol{\Sigma}|^{1/2}}\exp\left[-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})'\boldsymbol{\Sigma}(\boldsymbol{x}-\boldsymbol{\mu})\right], \tag{8.6} \end{equation}\] gdzie \(\boldsymbol{\mu}\) jest wektorem średnich \(\boldsymbol{x}\), a \(\boldsymbol{\Sigma}\) jest macierzą kowariancji \(\boldsymbol{x}\).

Uwaga. Liniowa kombinacja zmiennych losowych o normalnym rozkładzie łącznym ma również rozkład łączny normalny. W szczególności, jeśli \(A\) jest macierzą wymiaru \(d\times k\) i \(\boldsymbol{y} = A'\boldsymbol{x}\), to \(f(\boldsymbol{y})\sim N(A'\boldsymbol{\mu}, A'\boldsymbol{\Sigma}A)\). Odpowiednia forma macierzy przekształcenia \(A_w\), sprawia, że zmienne po transformacji charakteryzują się rozkładem normalnym łącznym o wariancji określonej przez \(I\). Jeśli \(\boldsymbol{\Phi}\) jest macierzą, której kolumny są ortonormalnymi wektorami własnymi macierzy \(\boldsymbol{\Sigma}\), a \(\boldsymbol{\Lambda}\) macierzą diagonalną wartości własnych, to transformacja \(A_w=\boldsymbol{\Phi}\boldsymbol{\Lambda}^{-1}\) przekształca \(\boldsymbol{x}\) w \(\boldsymbol{y}\sim N(A_w'\boldsymbol{\mu}, I)\).

Rysunek 8.4: Transformacje rozkładu normalnego łącznego. Źródło: Duda, Hart, and Stork (2001)

Definicja 8.1 Niech \(g_i(\boldsymbol{x}),\ i=1,\ldots,k\) będą pewnymi funkcjami dyskryminacyjnymi. Wówczas obiekt \(\boldsymbol{x}\) klasyfikujemy do grupy \(c_i\) jeśli spełniony jest warunek \[\begin{equation} g_i(\boldsymbol{x})>g_j(\boldsymbol{x}), \quad j\neq i. \end{equation}\]

W podejściu polegającym na minimalizacji prawdopodobieństwa błędnej klasyfikacji, przyjmuje się najczęściej, że \[\begin{equation} g_i(\boldsymbol{x})=\P(c_i|\boldsymbol{x}), \end{equation}\] czyli jako prawdopodobieństwo a posteriori. Wszystkie trzy poniższe postaci funkcji dyskryminacyjnych są dopuszczalne i równoważne ze względu na rezultat grupowania \[\begin{align} g_i(\boldsymbol{x})=&\P(c_i|\boldsymbol{x})=\frac{\P(\boldsymbol{x}|c_i)\P(c_i)}{\sum_{i=1}^k\P(\boldsymbol{x}|c_i)\P(c_i)},\\ g_i(\boldsymbol{x})=&\P(\boldsymbol{x}|c_i)\P(c_i),\\ g_i(\boldsymbol{x})=&\log\P(\boldsymbol{x}|c_i)+\log\P(c_i) \tag{8.7} \end{align}\] W przypadku gdy \(\boldsymbol{x}|c_i\sim N(\boldsymbol{\mu}_i, \boldsymbol{\Sigma}_i)\), to na podstawie (8.6) \(g_i\) danej jako (8.7) przyjmuje postać \[\begin{equation} g_i(\boldsymbol{x})=-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu}_i)'\boldsymbol{\Sigma}_i^{-1}(\boldsymbol{x}-\boldsymbol{\mu}_i)-\frac{d}{2}\log(2\pi)-\frac{1}{2}\log|\boldsymbol{\Sigma}_i|+\log\P(c_i). \end{equation}\]

W kolejnych podrozdziałach przeanalizujemy trzy możliwe formy macierzy kowariancji.

8.2.1 Przypadek gdy \(\boldsymbol{\Sigma}_i=\sigma^2I\)

To najprostszy przypadek, zakładający niezależność zmiennych wchodzących w skład \(\boldsymbol x\), których wariancje są stałe \(\sigma^2\). Wówczas \(g_i\) przyjmuje postać \[\begin{equation} g_i(\boldsymbol x)=-\frac{||\boldsymbol x-\boldsymbol \mu_i||^2}{2\sigma^2}+\log\P(c_i), \tag{8.8} \end{equation}\] gdzie \(||\cdot ||\) jest normą euklidesową.

Rozpisując licznik równania (8.8) mamy \[\begin{equation} ||\boldsymbol x-\boldsymbol \mu_i||^2=(\boldsymbol x-\boldsymbol \mu_i)'(\boldsymbol x-\boldsymbol \mu_i). \end{equation}\] Zatem \[\begin{equation} g_i(\boldsymbol x)=-\frac{1}{2\sigma^2}[\boldsymbol x'\boldsymbol x-2\boldsymbol \mu_i'\boldsymbol x+\boldsymbol \mu_i'\boldsymbol \mu_i]+\log\P(c_i). \end{equation}\] A ponieważ \(\boldsymbol x'\boldsymbol x\) nie zależy do \(i\), to funkcję dyskryminacyjną możemy zapisać jako \[\begin{equation} g_i(\boldsymbol x)=\boldsymbol w_i'\boldsymbol x+w_{i0}, \end{equation}\] gdzie \(\boldsymbol w_i=\frac{1}{\sigma^2}\boldsymbol \mu_i\), a \(w_{i0}=\frac{-1}{2\sigma^2}\boldsymbol \mu_i'\boldsymbol \mu_i+\log\P(c_i).\)

Na podstawie funkcji dyskryminacyjnych wyznaczamy hiperpłaszczyzny decyzyjne jako zbiory punktów dla których \(g_i(\boldsymbol x)=g_j(\boldsymbol x)\), gdzie \(g_i, g_j\) są największe. Możemy to zapisać w następujący sposób \[\begin{equation} \boldsymbol w'(\boldsymbol x-\boldsymbol x_0)=0, \tag{8.9} \end{equation}\] gdzie \[\begin{equation} \boldsymbol w = \boldsymbol \mu_i-\boldsymbol \mu_j, \end{equation}\] oraz \[\begin{equation} \boldsymbol x_0 = \frac12(\boldsymbol \mu_i+\boldsymbol\mu_j)-\frac{\sigma^2}{||\boldsymbol \mu_i-\boldsymbol \mu_j||^2}\log\frac{\P(c_i)}{\P(c_j)}(\boldsymbol \mu_i-\boldsymbol \mu_j). \end{equation}\]

Równanie (8.9) określa hiperpłaszczyznę przechodzącą przez \(\boldsymbol x_0\) i prostopadłą do \(\boldsymbol w\).

Rysunek 8.5: Dyskrymiancja hiperpłaszczyznami w sygucaji dwóch klas. Wykres po lewej, to ujęcie jednowymiarowe, wykresy po środu - ujęcie 2-wymiarowe i wykresy po prawej, to ujęcie 3-wymiarowe. Źródło: Duda, Hart, and Stork (2001)

8.2.2 Przypadek gdy \(\boldsymbol \Sigma_i=\boldsymbol \Sigma\)

Przypadek ten opisuje sytuację, gdy rozkłady \(\boldsymbol x\) są identyczne we wszystkich grupach ale zmienne w ich skład wchodzące nie są niezależne. W tym przypadku funkcje dyskryminacyjne przyjmują postać \[\begin{equation} g_i(\boldsymbol x)=\frac12(\boldsymbol x-\boldsymbol \mu_i)'\boldsymbol\Sigma^{-1}(\boldsymbol x-\boldsymbol \mu_i)+\log\P(c_i). \tag{8.10} \end{equation}\] Jeśli \(\P(c_i)\) są identyczne dla wszystkich klas, to można je pominąć we wzorze (8.10). Metryka euklidesowa ze wzoru (8.8) została zastąpiona przez odległość Mahalonobis’a. Podobnie ja w przypadku gdy \(\boldsymbol \Sigma_i=\sigma^2I\), tak i teraz można uprościć (8.10) przez rozpisanie formy kwadratowej, aby otrzymać, że \[\begin{equation} g_i(\boldsymbol x)=\boldsymbol w_i'\boldsymbol x+w_{i0}, \end{equation}\] gdzie \(\boldsymbol w_i=\boldsymbol\Sigma^{-1}\boldsymbol \mu_i\), a \(w_{i0}=-\frac{1}{2}\boldsymbol \mu_i'\boldsymbol\Sigma^{-1}\boldsymbol \mu_i+\log\P(c_i).\)

Ponieważ funkcje dyskryminacyjne są liniowe, to hiperpłaszczyzny są ograniczeniami obszarów obserwacji każdej z klas \[\begin{equation} \boldsymbol w'(\boldsymbol x-\boldsymbol x_0)=0, \tag{8.11} \end{equation}\] gdzie \[\begin{equation} \boldsymbol w = \boldsymbol\Sigma^{-1} (\boldsymbol \mu_i-\boldsymbol \mu_j), \end{equation}\] oraz \[\begin{equation} \boldsymbol x_0 = \frac12(\boldsymbol \mu_i+\boldsymbol\mu_j)-\frac{\log[ \P(c_i)/\P(c_j)]}{(\boldsymbol x-\boldsymbol \mu_i)'\boldsymbol\Sigma^{-1}(\boldsymbol x-\boldsymbol \mu_i)}(\boldsymbol \mu_i-\boldsymbol \mu_j). \end{equation}\] Tym razem \(\boldsymbol{w}=\Sigma^{-1}(\boldsymbol \mu_i-\boldsymbol \mu_j)\) nie jest wektorem w kierunku \(\boldsymbol \mu_i-\boldsymbol \mu_j\), więc hiperpłaszczyzna rozdzielająca obiekty różnych klas nie jest prostopadła do wektora \(\boldsymbol \mu_i-\boldsymbol \mu_j\) ale przecina go w połowie (w punkcie \(\boldsymbol x_0\)).

Rysunek 8.6: Hiperpłaszczyzna rozdzielająca obszary innych klas może być przesunięta w kierunku bardziej prawdopodobnej klasy, jeśli prawdopodobieństwa a priori są różne. Źródło: Duda, Hart, and Stork (2001)

8.2.3 Przypadek gdy \(\boldsymbol \Sigma_i\) jest dowolnej postaci

Jest to najbardziej ogólny przypadek, kiedy nie nakłada się żadnych ograniczeń na macierze kowariancji grupowych. Postać funkcji dyskryminacyjnych jest następująca \[\begin{equation} g_i(\boldsymbol x)=\boldsymbol x'\boldsymbol W_i\boldsymbol x+\boldsymbol w_i'\boldsymbol x+w_{i0} \tag{8.12} \end{equation}\] gdzie \[\begin{align} \boldsymbol W_i = &-\frac12 \boldsymbol\Sigma_i^{-1},\\ \boldsymbol w_i=& \boldsymbol\Sigma_i^{-1}\boldsymbol\mu_i,\\ w_{i0} = &-\frac12\boldsymbol\mu_i'\boldsymbol\Sigma_i^{-1}\boldsymbol\mu_i-\frac12\log|\boldsymbol\Sigma_i|+\log\P(c_i). \end{align}\]

Ograniczenia w ten sposób budowane są hiperpowierzchniami (nie koniecznie hiperpłaszczyznami). W literaturze ta metoda znana jest pod nazwą kwadratowej analizy dyskryminacyjnej (ang. Quadratic Discriminant Analysis).

Rysunek 8.7: Przykład zastosowania kwadratowej analizy dyskryminacyjnej. Pokazane są dopuszczalne postaci zbiorów ograniczających. Źródło: Duda, Hart, and Stork (2001)

Przykład 8.2 Przeprowadzimy klasyfikację na podstawie zbioru Smarket pakietu ILSR. Dane zawierają kursy indeksu giełdowego S&P500 w latach 2001-2005. Na podstawie wartości waloru z poprzednich 2 dni będziemy chcieli przewidzieć czy ruch w kolejnym okresie czasu będzie w górę czy w dół.

library(ISLR)
head(Smarket)

##   Year   Lag1   Lag2   Lag3   Lag4   Lag5 Volume  Today Direction
## 1 2001  0.381 -0.192 -2.624 -1.055  5.010 1.1913  0.959        Up
## 2 2001  0.959  0.381 -0.192 -2.624 -1.055 1.2965  1.032        Up
## 3 2001  1.032  0.959  0.381 -0.192 -2.624 1.4112 -0.623      Down
## 4 2001 -0.623  1.032  0.959  0.381 -0.192 1.2760  0.614        Up
## 5 2001  0.614 -0.623  1.032  0.959  0.381 1.2057  0.213        Up
## 6 2001  0.213  0.614 -0.623  1.032  0.959 1.3491  1.392        Up

set.seed(44)
dt.ucz <- Smarket %>% 
    mutate_if(is.numeric, scale) %>% 
    sample_frac(size = 2/3) 
dt.test <- Smarket[-as.numeric(rownames(dt.ucz)),]
mod.qda <- qda(Direction~Lag1+Lag2, data = dt.ucz)
mod.qda

## Call:
## qda(Direction ~ Lag1 + Lag2, data = dt.ucz)
## 
## Prior probabilities of groups:
##      Down        Up 
## 0.4909964 0.5090036 
## 
## Group means:
##            Lag1        Lag2
## Down  0.0328367  0.06722714
## Up   -0.0671615 -0.08814914

Ponieważ funkcje dyskryminacyjne mogą być nieliniowe, to podsumowanie modelu nie zawiera współczynników funkcji. Podsumowanie zawiera tylko prawdopodobieństwa a priori i średnie poszczególnych zmiennych niezależnych w klasach.

pred.qda <- predict(mod.qda, dt.test)
tab <- table(pred = pred.qda$class, dt.test$Direction)
tab

##       
## pred   Down  Up
##   Down   42  34
##   Up    139 202

sum(diag(prop.table(tab)))

## [1] 0.5851319

library(klaR)
partimat(Direction ~ Lag1+Lag2, 
         data = dt.ucz,
         method = "qda",
         col.correct='blue',
         col.wrong='red')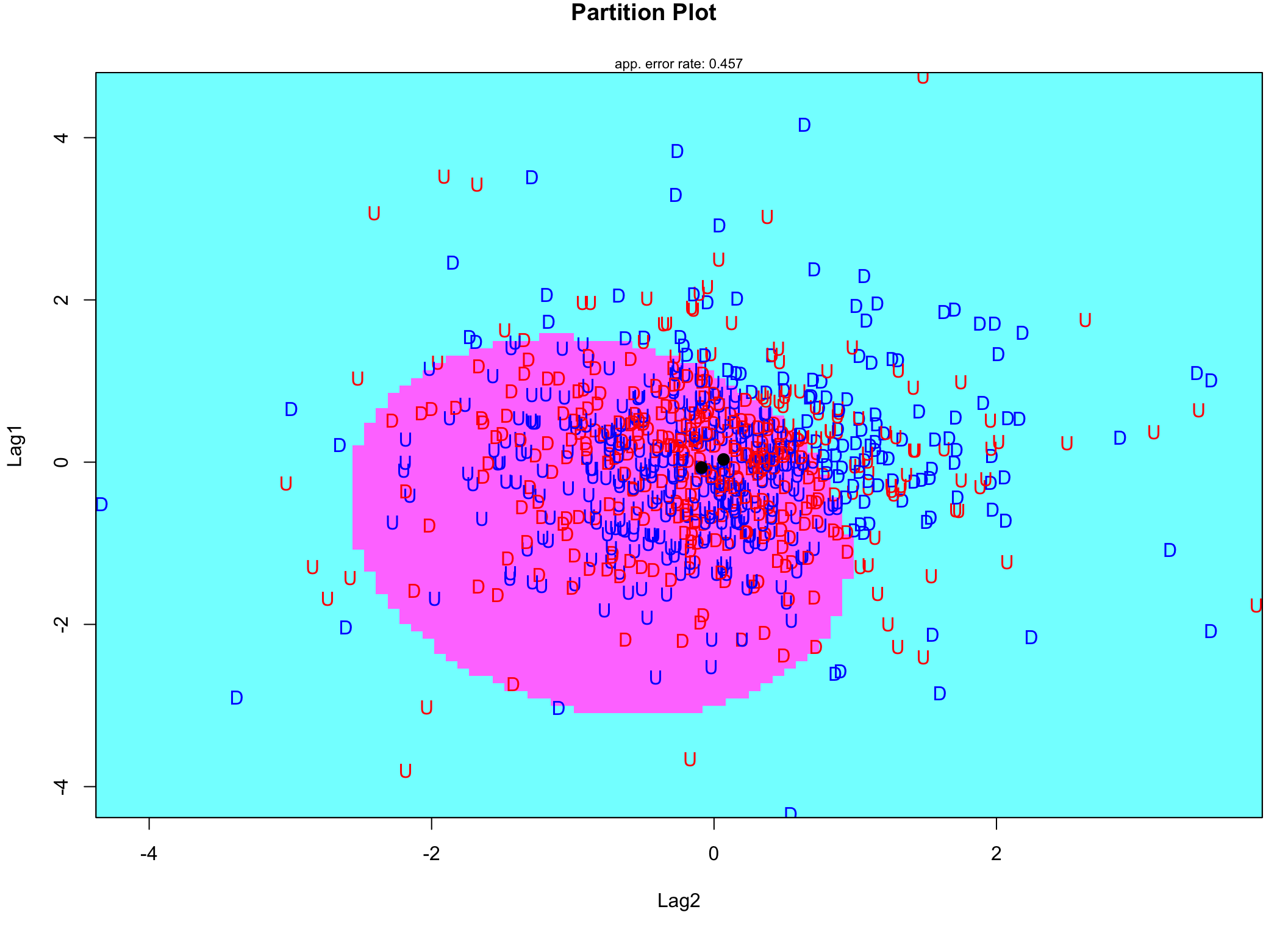

Rysunek 8.8: Wykres klasyfikacji na podstawie QDA. Obserwacje zaznczone kolorem niebieskim są prawidłowo zaklasyfikowane, a czerwonym źle

8.3 Analiza dyskryminacyjna metodą częściowych najmniejszych kwadratów

Analiza dyskryminacyjna metodą częściowych najmniejszych kwadratów (ang. Partial Least Squares Discriminant Analysis) jest wykorzystywana szczególnie w sytuacjach gdy zestaw predyktorów zwiera zmienne silnie ze sobą skorelowane. Jak wiadomo z wcześniejszych rozważań, metody dyskryminacji obserwacji są mało odporne na nadmiarowość zmiennych niezależnych. Stąd powstał pomysł zastosowania połączenia LDA z PLS (Partial Least Squares), której celem jest redukcja wymiaru przestrzeni jednocześnie maksymalizując korelację zmiennych niezależnych ze zmienną wynikową.

Parametrem, który jest kontrolowany podczas budowy modelu jest liczba ukrytych zmiennych. Metoda PLSDA ma kilka implementacji w R, ale najbardziej znana jest funkcja plsda z pakietu caret (Jed Wing et al. 2018).

Przykład 8.3 Kontynując poprzedni przykład przeprowadzimy klasyfikacje ruchu waloru korzystając z metody PLSDA. W przeciwieństwie do poprzednich funkcji plsda potrzebuje przekazania zbioru predyktorów i wektora zmiennej wynikowej oddzielnie, a nie za pomocą formuły. Doboru liczby zmiennych latentnych dokonamy arbitralnie.

library(caret)
mod.plsda <- plsda(dt.ucz[,-c(1,7:9)],
                   as.factor(dt.ucz$Direction), 
                   ncomp = 2)
mod.plsda$loadings

## 
## Loadings:
##      Comp 1 Comp 2
## Lag1 -0.548  0.375
## Lag2 -0.805 -0.204
## Lag3        -0.520
## Lag4 -0.143  0.652
## Lag5  0.186  0.351
## 
##                Comp 1 Comp 2
## SS loadings     1.004  1.001
## Proportion Var  0.201  0.200
## Cumulative Var  0.201  0.401

Dwie ukryte zmienne użyte do redukcji wymiaru przestrzeni wyjaśniają około 40% zmienności pierwotnych zmiennych. Ładunki (Loadings) pokazują kontrybucje poszczególnych zmiennych w tworzenie się zmiennych ukrytych.

pred.plsda <- predict(mod.plsda, dt.test[,-c(1,7:9)])
tab <- table(pred.plsda, dt.test$Direction)
tab

##           
## pred.plsda Down  Up
##       Down   87  97
##       Up     94 139

sum(diag(prop.table(tab)))

## [1] 0.5419664

Ponieważ korelacje pomiędzy predyktorami w naszym przypadku nie były duże, to zastosowanie PLSDA nie poprawiło klasyfikacji w stosunku do metody QDA.

cor(dt.ucz[,2:6])

##              Lag1         Lag2         Lag3        Lag4        Lag5
## Lag1  1.000000000 -0.003318026 -0.004329303  0.02574559  0.01831679
## Lag2 -0.003318026  1.000000000 -0.057166931  0.01209305  0.02127975
## Lag3 -0.004329303 -0.057166931  1.000000000  0.01574896 -0.07541592
## Lag4  0.025745592  0.012093049  0.015748958  1.00000000 -0.04607207
## Lag5  0.018316786  0.021279754 -0.075415921 -0.04607207  1.00000000

8.4 Regularyzowana analiza dyskryminacyjna

Regularyzowana analiza dyskryminacyjna (ang. Regularized Discriminant Analysis) powstała jako technika równoważąca zalety i wady LDA i QDA. Ze względu na zdolności generalizacyjne model LDA jest lepszy od QDA (mniejsza wariancja modelu), ale jednocześnie QDA ma bardziej elastyczną postać hiperpowierzchni brzegowych rozdzielających obiekty różnych klas. Dlatego Friedman -Friedman (1989) wprowadził technikę będącą kompromisem pomiędzy LDA i QDA poprzez odpowiednie określenie macierzy kowariancji \[\begin{equation} \tilde{\boldsymbol \Sigma}_i(\lambda) = \lambda\boldsymbol\Sigma_i + (1-\lambda)\boldsymbol\Sigma, \end{equation}\] gdzie \(\boldsymbol \Sigma_i\) jest macierzą kowariancji dla \(i\)-tej klasy, a \(\boldsymbol \Sigma\) jest uśrednioną macierzą kowariancji wszystkich klas. Zatem odpowiedni dobór parametru \(\lambda\) decyduje czy poszukujemy modelu prostszego (\(\lambda = 0\) odpowiada LDA), czy bardziej elastycznego (\(\lambda=1\) oznacza QDA).

Dodatkowo metoda RDA pozwala na elastyczny wybór pomiędzy postaciami macierzy kowariancji wspólnej dla wszystkich klas \(\boldsymbol\Sigma\). Może ona być macierzą jednostkową, jak w przypadku 8.2.1, co oznacza niezależność predyktorów modelu, może też być jak w przypadku 8.2.2, gdzie dopuszcza się korelacje między predyktorami. Dokonuje się tego przez odpowiedni dobór parametru \(\gamma\) \[\begin{equation} \boldsymbol \Sigma(\gamma) = \gamma\boldsymbol \Sigma+(1-\gamma)\sigma^2I. \end{equation}\]

Przykład 8.4 Funkcja rda pakietu klaR jest implementacją powyższej metody. Ilustrają jej działania będzie klasyfikacja stanów z poprzedniego przykładu.

library(klaR)
mod.rda <- rda(Direction~Lag1+Lag2+Lag3+Lag4+Lag5, dt.ucz)
mod.rda

## Call: 
## rda(formula = Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5, data = dt.ucz)
## 
## Regularization parameters: 
##       gamma      lambda 
## 0.713621809 0.004013224 
## 
## Prior probabilities of groups: 
##      Down        Up 
## 0.4909964 0.5090036 
## 
## Misclassification rate: 
##        apparent: 44.058 %
## cross-validated: 46.482 %

Model został oszacowany z parametrami wyznaczonymi na podstawie sprawdzianu krzyżowego zastosowanego w funkcji rda.

pred.rda <- predict(mod.rda, dt.test)
(tab <- table(pred = pred.rda$class, dt.test$Direction))

##       
## pred   Down  Up
##   Down   24  31
##   Up    157 205

sum(diag(prop.table(tab)))

## [1] 0.5491607

Jakość klasyfikacji jest na zbliżonym poziomie jak przy poprzednich metodach.

8.5 Analiza dyskryminacyjna mieszana

Liniowa analiza dyskryminacyjna zakładała, że średnie (centroidy) w klasach są różne ale macierz kowariancji wszystkich klas jest jednakowa. Analiza dyskryminacyjna mieszana (ang. Mixture Discriminant Analysis) prezentuje jeszcze inne podejście ponieważ zakłada, że każda klasa może być charakteryzowana przez wiele wielowymiarowych rozkładów normalnych, których centroidy mogą się różnic, ale macierze kowariancji nie.

Wówczas rozkład dla danej klasy jest mieszaniną rozkładów składowych, a funkcja dyskryminacyjna dla \(i\)-tej klasy przyjmuje postać \[\begin{equation} g_i(\boldsymbol x)\propto \sum_{k=1}^{L_i}\phi_{ik}g_{ik}(\boldsymbol x), \end{equation}\] gdzie \(L_i\) jest liczbą rozkładów składających się na \(i\)-tą klasę, a \(\phi_{ik}\) jest współczynnikiem proporcji estymowanych w czasie uczenia modelu.

Przykład 8.5 Funkcja mda pakietu mda (Trevor Hastie et al. 2017) jest implementacją tej techniki w R. Jej zastosowanie pokażemy na przykładzie danych giełdowych z poprzedniego przykładu. Użyjemy domyślnych ustawień funkcji (trzy rozkłady dla każdej klasy).

library(mda)
mod.mda <- mda(Direction~Lag1+Lag2+Lag3+Lag4+Lag5, dt.ucz)
mod.mda

## Call:
## mda(formula = Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5, data = dt.ucz)
## 
## Dimension: 5 
## 
## Percent Between-Group Variance Explained:
##     v1     v2     v3     v4     v5 
##  63.78  95.81  98.97  99.84 100.00 
## 
## Degrees of Freedom (per dimension): 6 
## 
## Training Misclassification Error: 0.43337 ( N = 833 )
## 
## Deviance: 1134.288

pred.mda <- predict(mod.mda, dt.test)
(tab <- table(pred = pred.mda, dt.test$Direction))

##       
## pred   Down  Up
##   Down   38  46
##   Up    143 190

sum(diag(prop.table(tab)))

## [1] 0.5467626

Kolejny raz model dyskryminacyjny charakteryzuje się podobną jakością klasyfikacji.

8.6 Elastyczna analiza dyskryminacyjna

Zupełnie inne podejście w stosunku do wcześniejszych rozwiązań, prezentuje elastyczna analiza dyskryminacyjna (ang. Flexible Discriminant Analysis) . Kodując klasy wynikowe jako zmienne dychotomiczne (dla każdej klasy jest odrębna zmienna wynikowa) dla każdej z nich budowanych jest \(k\) modeli regresji. Mogą to być modele regresji penalizowanej, jak regresja grzbietowa lub LASSO, modele regresji wielomianowej albo modele regresji sklejanej (MARS), o których będzie mowa w dalszej części tego opracowania.

Przykładowo, jeśli modelem bazowym jest MARS, to funkcja dyskryminacyjna \(i\)-tej klasy może być postaci \[\begin{equation} g_i(\boldsymbol x)=\beta_0+\beta_1h(1-x_1)+\beta_2h(x_2-1)+\beta_3h(1-x_3)+\beta_4h(x_1-1), \end{equation}\] gdzie \(h\) są tzw. funkcjami bazowymi postaci \[\begin{equation} h(x)= \begin{cases} x, & x> 0\\ 0, & x\leq 0. \end{cases} \end{equation}\] Klasyfikacji dokonujemy sprawdzając znak funkcji dyskryminacyjnej \(g_i\), jeśli jest dodatni, to funkcja przypisuje obiekt do klasy \(i\)-tej. W przeciwnym przypadku nie należy do tej klasy.

Rysunek 8.9: Przykład klasyfikacji dwustanowej za pomocą metody FDA

Przykład 8.6 Funkcja fda pakietu mda jest implementacją techniki FDA w R. Na postawie danych z poprzedniego przykładu zostanie przedstawiona zasada dziełania. Przyjmiemy domyślne ustawienia funkcji, z wyjątkiem metody estymacji modelu, jako którą przyjmiemy MARS.

mod.fda <- fda(Direction ~ Lag1+Lag2, dt.ucz, method = mars)
mod.fda

## Call:
## fda(formula = Direction ~ Lag1 + Lag2, data = dt.ucz, method = mars)
## 
## Dimension: 1 
## 
## Percent Between-Group Variance Explained:
##  v1 
## 100 
## 
## Training Misclassification Error: 0.44418 ( N = 833 )

Ponieważ, zmienna wynikowa jest dwustanowa, to powstała tylko jedna funkcja dyskryminacyjna. Parametry modelu są następujące

mod.fda$fit$coefficients

##             [,1]
## [1,]  0.05846465
## [2,] -0.17936208

pred.fda <- predict(mod.fda, dt.test)
(tab <- table(pred = pred.fda, dt.test$Direction))

##       
## pred   Down  Up
##   Down   40  50
##   Up    141 186

sum(diag(prop.table(tab)))

## [1] 0.5419664

Jakość klasyfikacji jest tylko nieco lepsza niż w przypadku poprzednich metod.

Bibliografia

Duda, Richard O., Peter E. Hart, and David G. Stork. 2001. Pattern Classification. Wiley. https://books.google.com?id=YoxQAAAAMAAJ.

Fisher, R. A. 1936. “The Use of Multiple Measurements in Taxonomic Problems.” Annals of Eugenics 7 (2): 179–88. https://doi.org/10.1111/j.1469-1809.1936.tb02137.x.

Friedman, Jerome H. 1989. “Regularized Discriminant Analysis.” Journal of the American Statistical Association 84 (405): 165–75. https://doi.org/10.2307/2289860.

Jed Wing, Max Kuhn. Contributions from, Steve Weston, Andre Williams, Chris Keefer, Allan Engelhardt, Tony Cooper, Zachary Mayer, et al. 2018. Caret: Classification and Regression Training. https://CRAN.R-project.org/package=caret.

Trevor Hastie, S original by, Robert Tibshirani. Original R port by Friedrich Leisch, Kurt Hornik, and Brian D. Ripley. 2017. Mda: Mixture and Flexible Discriminant Analysis. https://CRAN.R-project.org/package=mda.

Welch, B. L. 1939. “Note on Discriminant Functions.” Biometrika 31 (1/2): 218–20. https://doi.org/10.2307/2334985.