10 Metoda \(k\) najbliższych sąsiadów
Technika \(k\) najbliższych sąsiadów (ang. \(k\)-Nearest Neighbors) przewiduje wartość zmiennej wynikowej na podstawie \(k\) najbliższych obserwacji zbioru uczącego. W przeciwieństwie do wspomnianych wcześniej modeli liniowych, nie posiada ona jawnej formy i należy do klasy technik nazywanych czarnymi skrzynkami (ang. black box). Może być wykorzystywana, zarówno do zadań klasyfikacyjnych, jak i regresyjnych. W obu przypadkach predykcja dla nowych wartości predyktorów przebiega podobnie.
Niech \(\boldsymbol x_0\) będzie obserwacją, dla której poszukujemy wartości zmiennej wynikowej \(y_0\). Na podstawie zbioru obserwacji \(\boldsymbol x\in T\) zbioru uczącego wyznacza się \(k\) najbliższych sąsiadów19, gdzie \(k\) jest z góry ustaloną wartością. Następnie, jeśli zadanie ma charakter klasyfikacyjny, to \(y_0\) przypisuje się modę zmiennej wynikowej obserwacji będących \(k\) najbliższymi sąsiadami. W przypadku zadań regresyjnych \(y_0\) przypisuje się średnią lub medianę.
Olbrzymie znaczenie dla wyników predykcji na podstawie metody kNN ma dobór metryki. Nie istnieje obiektywna technika wyboru najlepszej metryki, dlatego jej doboru dokonujemy metodą prób i błędów. Należy dodatkowo pamiętać, że wielkości mierzone \(\boldsymbol x\) mogą się różnić zakresami zmienności, a co za tym idzie, mogą znacząco wpłynąć na mierzone odległości pomiędzy punktami. Dlatego zaleca się standaryzację zmiennych przed zastosowaniem metody kNN.
Kolejnym parametrem, który ma znaczący wpływ na predykcję, jest liczba sąsiadów \(k\). Wybór zbyt małej liczby \(k\) może doprowadzić do przeuczenia modelu jak to jest pokazane na rysunku 10.1
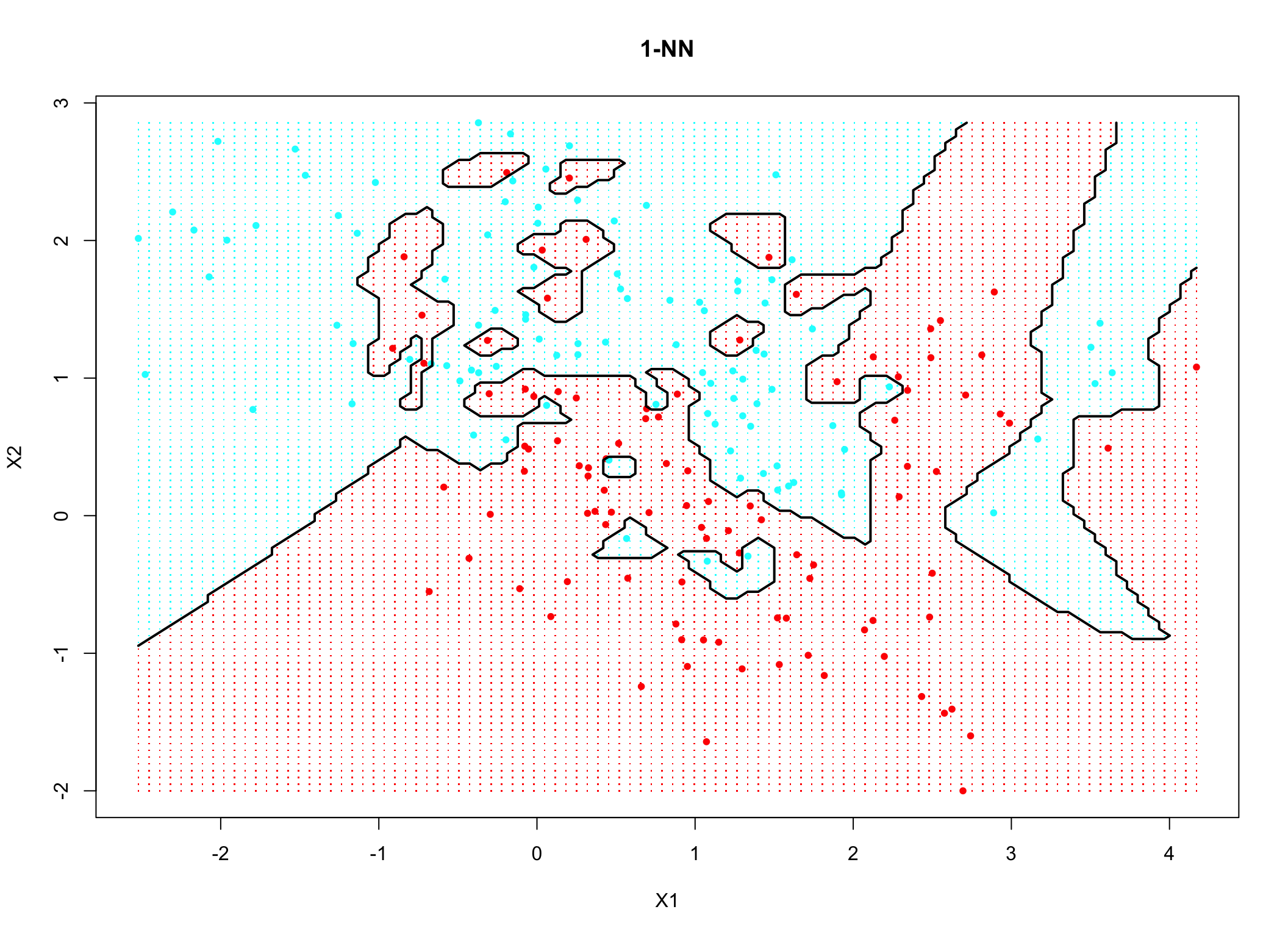
Rysunek 10.1: Przykład klasyfikacji dla \(k=1\)
Z kolei zbyt duża liczba sąsiadów powoduje obciążenie wyników (patrz rysunek 10.2)
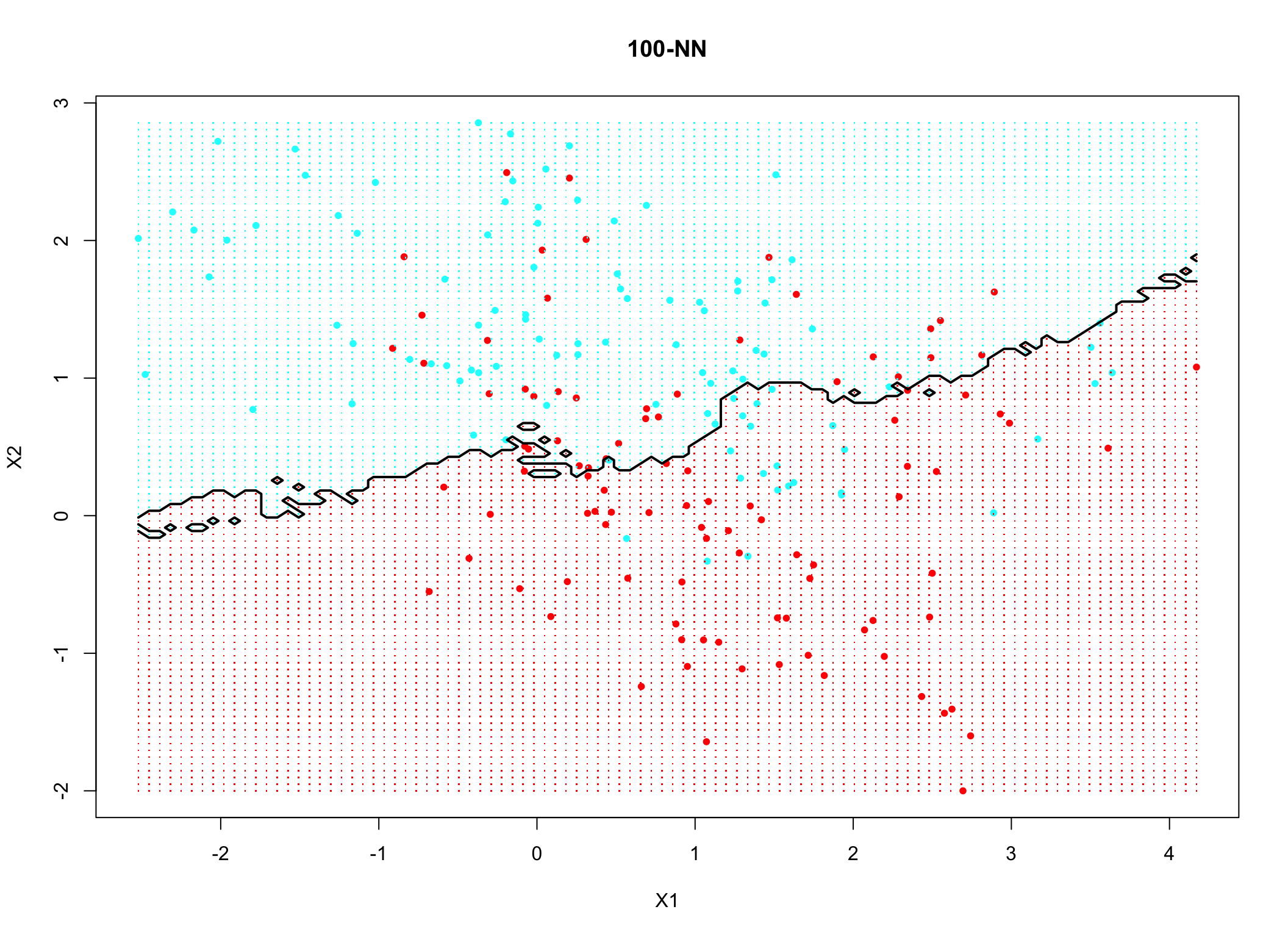
Rysunek 10.2: Przykład zastosowania 100 sąsiadów
Dopiero dobór odpowiedniego \(k\) daje model o stosunkowo niskiej wariancji i obciążeniu. Najczęściej liczby \(k\) poszukujemy za pomocą próbkowania.
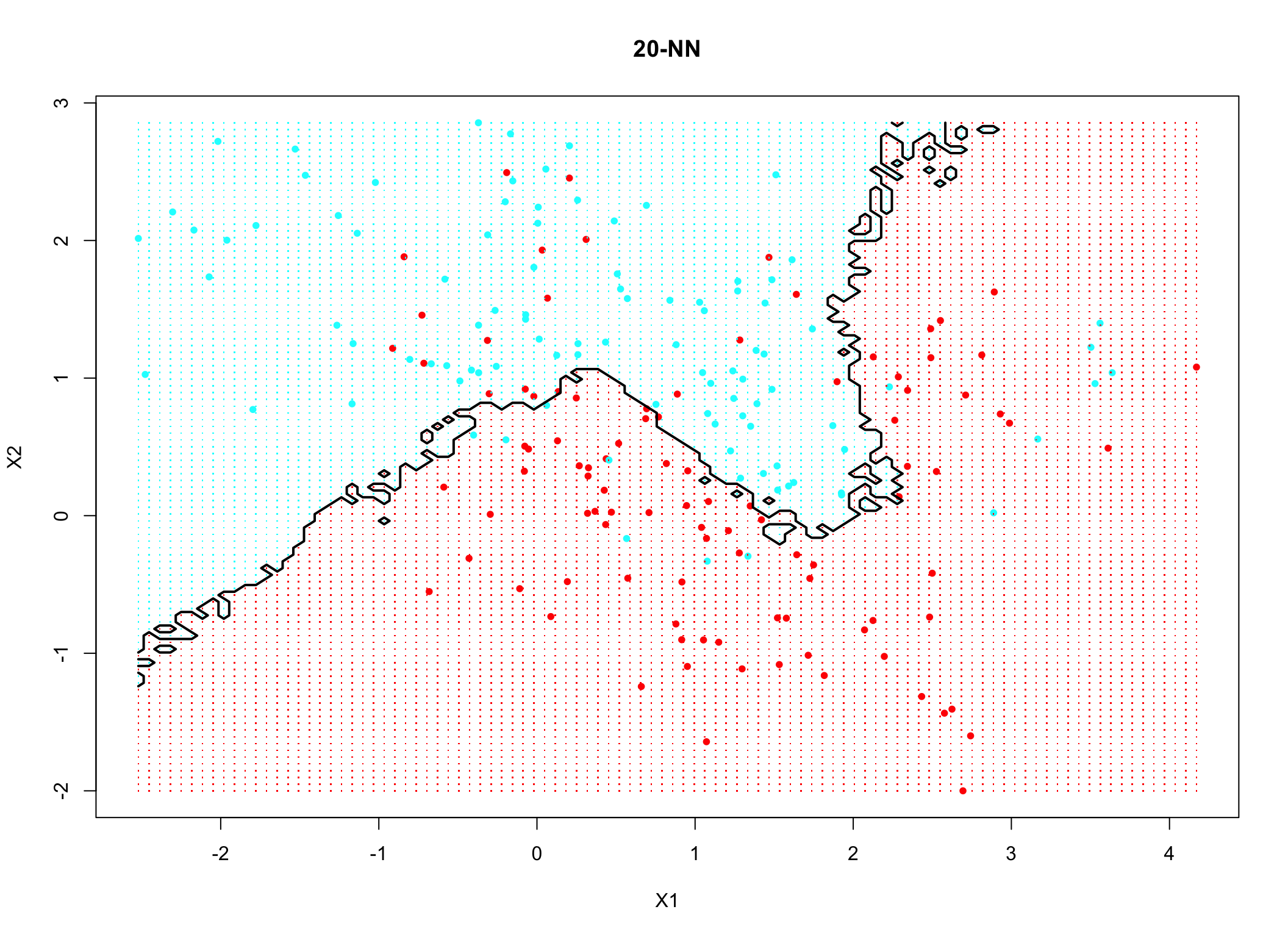
Rysunek 10.3: Model z optymalną liczbą sąsiadów
Przykład 10.1 Klasyfikację z wykorzystaniem metody kNN przeprowadzimy na przykładzie danych zbioru spam ze strony spambase. Metoda kNN ma wiele implementacji R-owych ale na potrzeby przykładu wykorzystamy funkcję knn3 pakietu caret.
Najpierw dokonamy oszacowania optymalnego \(k\)
library(tidyverse)
spam <- read.csv("spam.csv")
spam <- spam[,-1] # usuwam licznik wierszy
names(spam)[58] <- "spam"
spam$spam <- as.factor(spam$spam)
spam.std <- spam %>%
mutate_if(is.numeric, scale)
set.seed(123)
ind <- sample(nrow(spam), size = nrow(spam)*2/3)
dt.ucz <- spam.std[ind,]
dt.test <- spam.std[-ind,]
acc <- function(pred, obs){
tab <- table(pred,obs)
acc <- sum(diag(prop.table(tab)))
acc
}
1:40 %>%
map(~knn3(spam~., data = dt.ucz, k = .x)) %>%
map(~predict(.x, newdata = dt.test, type = "class")) %>%
map_dbl(~acc(pred = .x, obs = dt.test$spam)) %>%
tibble(k = 1:length(.), acc=.) %>%
ggplot(aes(k, acc))+
geom_line()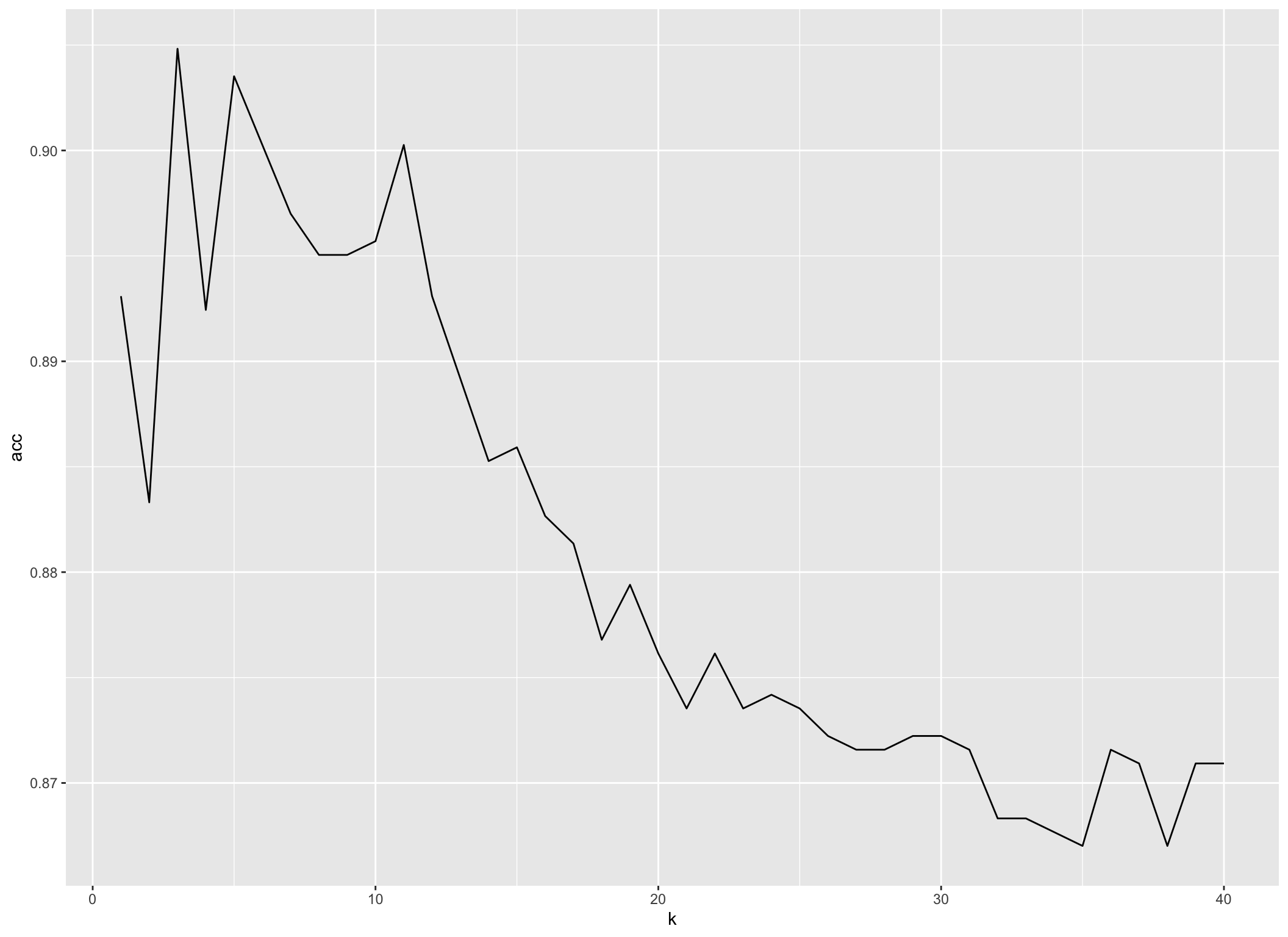
Rysunek 10.4: Ocena jakości dopasowania modelu dla różnej liczby sąsiadów
Biorąc pod uwagę wykres 10.4 można rozważać 3 lub 5 sąsiadów jako optymalne rozwiązanie, ponieważ wówczas poprawność klasyfikacji jest najwyższa. Proponuje unikać rozwiązania z 1 najbliższym sąsiadem ponieważ, będzie się ono charakteryzowało duża zmiennością. Wybór \(k=3\) wydaje się być optymalny.
## 3-nearest neighbor model
## Training set outcome distribution:
##
## 0 1
## 1860 1207Predykcji dokonujemy w ten sam sposób co w innych modelach klasyfikacyjnych
## [1] 1 1 1 1 1 1
## Levels: 0 1## 0 1
## [1,] 0.0000000 1.0000000
## [2,] 0.3333333 0.6666667
## [3,] 0.3333333 0.6666667
## [4,] 0.0000000 1.0000000
## [5,] 0.3333333 0.6666667
## [6,] 0.0000000 1.0000000##
## pred.knn.class 0 1
## 0 869 88
## 1 59 518## [1] 0.9041721metrykę można wybierać dowolnie, choć najczęściej jest to metryka euklidesowa↩︎