5 Pochodne drzew decyzyjnych

Przykład zastosowania drzew decyzyjnych na zbiorze iris w poprzednich przykładach może skłaniać do przypuszczenia, że drzewa decyzyjne zawsze dobrze radzą sobie z predykcją wartości wynikowej. Niestety w przykładach nieco bardziej skomplikowanych, gdzie chociażby klasy zmiennej wynikowej nie są tak wyraźnie separowalne, drzewa decyzyjne wypadają gorzej w porównaniu z innymi modelami nadzorowanego uczenia maszynowego.

I tak u podstaw metod bazujących na prostych drzewach decyzyjnych stał pomysł, że skoro jedno drzewo nie ma wystarczających własności predykcyjnych, to może zastosowanie wielu drzew połączonych w pewien sposób poprawi je. Tak powstały metody bagging, random forest i boosting17. Należy zaznaczyć, że metody znajdują swoje zastosowanie również w innych modelach nadzorowanego uczenia maszynowego.

5.1 Bagging

Technika ta została wprowadzona przez Breiman (1996) i ma na celu zmniejszenie wariancji modelu pojedynczego drzewa. Podobnie jak technika bootstrap, w której statystyki są wyliczane na wielu próbach pobranych z tego samego rozkładu (próby), w metodzie bagging losuje się wiele prób ze zbioru uczącego (najczęściej poprzez wielokrotne losowanie próby o rozmiarze zbioru uczącego ze zwracaniem), a następnie dla każdej próby bootstrapowej buduje się drzewo. W ten sposób otrzymujemy \(B\) drzew decyzyjnych \(\hat{f}^1(x), \hat{f}^2(x),\ldots, \hat{f}^B(x)\). Na koniec poprzez uśrednienie otrzymujemy model charakteryzujący się większą precyzją \[\begin{equation} \hat{f}_{bag}(x)=\frac1B\sum_{b=1}^B\hat{f}^b(x). \end{equation}\]

Ponieważ podczas budowy drzew na podstawie prób bootstrapowych nie kontrolujemy złożoności, to w rezultacie każde z drzew może charakteryzować się dużą wariancją. Poprzez uśrednianie wyników pojedynczych drzew otrzymujemy mniejsze obciążenie ale również przy dostatecznie dużej liczbie prób (\(B\) często liczy się w setkach, czy tysiącach) zmniejszamy wariancję “średniej” predykcji z drzew. Oczywiście metodę tą trzeba dostosować do zadań klasyfikacyjnych, ponieważ nie istnieje średnia klasyfikacji z wielu drzew. W miejsce średniej stosuje się modę, czyli wartość dominującą.

Przyjrzyjmy się jak maszyna losuje obserwacje ze zwracaniem

n <- NULL
m <- NULL
for(i in 1:1000){
    x <- sample(1:500, size = 500, replace = T)
    y <- setdiff(1:500, x)
    z <- unique(x)
    n[i] <- length(z)
    m[i] <- length(y)
}
mean(n)/500*100
## [1] 63.2802
mean(m)/500*100
## [1] 36.7198

Faktycznie uczenie modelu metodą bagging odbywa się średnio na 2/3 obserwacji zbioru uczącego wylosowanych do prób bootstrapowych, a pozostała 1/3 (ang. out-of-bag) jest wykorzystana do oceny jakości predykcji.

Niewątpliwą zaletą drzew decyzyjnych była ich łatwa interpretacja. W przypadku metody bagging jest ona znacznie utrudniona, ponieważ jej wynik składa się z agregacji wielu drzew. Można natomiast ocenić ważność predyktorów (ang. variable importance). I tak, przez obserwację spadku \(RSS\) dla baggingu regresyjnego przy zastosowaniu danego predyktora w podziałach drzewa i uśrednieniu wyniku otrzymamy wskaźnik ważności predyktora dużo lepszy niż dla pojedynczego drzewa. W przypadku baggingu klasyfikacyjnego w miejsce \(RSS\) stosujemy indeks Gini’ego.

Implementacja R-owa metody bagging znajduje się w pakiecie ipred, a funkcja do budowy modelu nazywa się bagging (Peters and Hothorn 2018). Można również stosować funkcję randomForest pakietu randomForest (Liaw and Wiener 2002) - powody takiego działania wyjaśnią się w podrozdziale Lasy losowe.

Przykład 5.1 Tym razem cel zadania jest regresyjny i polega na ustaleniu miary tendencji centralnej ceny mieszkań w Bostonie na podstawie zmiennych umieszczonych w zbiorze Boston pakietu MASS (Venables and Ripley 2002). Zmienną zależną będzie mediana cen mieszkań na przedmieściach Bostonu (medv).

library(MASS)
head(Boston)
##      crim zn indus chas   nox    rm  age    dis rad tax ptratio  black lstat
## 1 0.00632 18  2.31    0 0.538 6.575 65.2 4.0900   1 296    15.3 396.90  4.98
## 2 0.02731  0  7.07    0 0.469 6.421 78.9 4.9671   2 242    17.8 396.90  9.14
## 3 0.02729  0  7.07    0 0.469 7.185 61.1 4.9671   2 242    17.8 392.83  4.03
## 4 0.03237  0  2.18    0 0.458 6.998 45.8 6.0622   3 222    18.7 394.63  2.94
## 5 0.06905  0  2.18    0 0.458 7.147 54.2 6.0622   3 222    18.7 396.90  5.33
## 6 0.02985  0  2.18    0 0.458 6.430 58.7 6.0622   3 222    18.7 394.12  5.21
##   medv
## 1 24.0
## 2 21.6
## 3 34.7
## 4 33.4
## 5 36.2
## 6 28.7
set.seed(2019)
boston.train <- Boston %>% 
    sample_frac(size = 2/3)
boston.test <- setdiff(Boston, boston.train)

Aby móc porównać wyniki predykcji z metody bagging, najpierw zostanie zbudowane jedno drzewo decyzyjne w oparciu o algorytm CART.

library(rpart)
library(rpart.plot)
boston.rpart <- rpart(medv~., data = boston.train)
x <- summary(boston.rpart)
## Call:
## rpart(formula = medv ~ ., data = boston.train)
##   n= 337 
## 
##           CP nsplit rel error    xerror       xstd
## 1 0.49839799      0 1.0000000 1.0086928 0.10259521
## 2 0.15725128      1 0.5016020 0.5442932 0.06125724
## 3 0.07485605      2 0.3443507 0.4031978 0.05139310
## 4 0.03672387      3 0.2694947 0.3127794 0.04599170
## 5 0.03552748      4 0.2327708 0.2974517 0.04560807
## 6 0.01695185      5 0.1972433 0.2553208 0.04022970
## 7 0.01422576      6 0.1802915 0.2713816 0.04099092
## 8 0.01103490      7 0.1660657 0.2744789 0.04107777
## 9 0.01000000      8 0.1550308 0.2720415 0.04119266
## 
## Variable importance
##      rm   lstat   indus ptratio    crim     age     nox     dis      zn     tax 
##      33      19       9       8       7       6       6       5       3       2 
##     rad    chas 
##       1       1 
## 
## Node number 1: 337 observations,    complexity param=0.498398
##   mean=22.69792, MSE=79.32964 
##   left son=2 (286 obs) right son=3 (51 obs)
##   Primary splits:
##       rm      < 6.92     to the left,  improve=0.4983980, (0 missing)
##       lstat   < 9.725    to the right, improve=0.4424796, (0 missing)
##       indus   < 6.66     to the right, improve=0.2796065, (0 missing)
##       ptratio < 19.65    to the right, improve=0.2600149, (0 missing)
##       nox     < 0.6695   to the right, improve=0.2346383, (0 missing)
##   Surrogate splits:
##       ptratio < 14.55    to the right, agree=0.884, adj=0.235, (0 split)
##       lstat   < 4.915    to the right, agree=0.878, adj=0.196, (0 split)
##       zn      < 87.5     to the left,  agree=0.864, adj=0.098, (0 split)
##       indus   < 1.605    to the right, agree=0.864, adj=0.098, (0 split)
##       crim    < 0.013355 to the right, agree=0.852, adj=0.020, (0 split)
## 
## Node number 2: 286 observations,    complexity param=0.1572513
##   mean=20.04266, MSE=37.17489 
##   left son=4 (114 obs) right son=5 (172 obs)
##   Primary splits:
##       lstat   < 14.405   to the right, improve=0.3954065, (0 missing)
##       nox     < 0.6695   to the right, improve=0.3012249, (0 missing)
##       crim    < 8.37969  to the right, improve=0.2817286, (0 missing)
##       ptratio < 20.15    to the right, improve=0.2392532, (0 missing)
##       dis     < 2.4737   to the left,  improve=0.2295258, (0 missing)
##   Surrogate splits:
##       age   < 84.3     to the right, agree=0.808, adj=0.518, (0 split)
##       dis   < 2.23935  to the left,  agree=0.773, adj=0.430, (0 split)
##       crim  < 4.067905 to the right, agree=0.762, adj=0.404, (0 split)
##       nox   < 0.5765   to the right, agree=0.762, adj=0.404, (0 split)
##       indus < 16.57    to the right, agree=0.759, adj=0.395, (0 split)
## 
## Node number 3: 51 observations,    complexity param=0.07485605
##   mean=37.58824, MSE=54.4677 
##   left son=6 (34 obs) right son=7 (17 obs)
##   Primary splits:
##       rm      < 7.47     to the left,  improve=0.72041550, (0 missing)
##       lstat   < 3.99     to the right, improve=0.34223650, (0 missing)
##       ptratio < 15.05    to the right, improve=0.21227430, (0 missing)
##       rad     < 2.5      to the left,  improve=0.10053340, (0 missing)
##       tax     < 267      to the right, improve=0.07935891, (0 missing)
##   Surrogate splits:
##       lstat < 3.99     to the right, agree=0.824, adj=0.471, (0 split)
##       indus < 1.215    to the right, agree=0.706, adj=0.118, (0 split)
##       chas  < 0.5      to the left,  agree=0.706, adj=0.118, (0 split)
##       tax   < 225      to the right, agree=0.706, adj=0.118, (0 split)
##       crim  < 1.3713   to the left,  agree=0.686, adj=0.059, (0 split)
## 
## Node number 4: 114 observations,    complexity param=0.03552748
##   mean=15.33333, MSE=21.50994 
##   left son=8 (77 obs) right son=9 (37 obs)
##   Primary splits:
##       crim    < 0.69916  to the right, improve=0.3873341, (0 missing)
##       nox     < 0.6615   to the right, improve=0.3541892, (0 missing)
##       dis     < 2.3497   to the left,  improve=0.3182514, (0 missing)
##       ptratio < 19.45    to the right, improve=0.3102781, (0 missing)
##       tax     < 567.5    to the right, improve=0.2823826, (0 missing)
##   Surrogate splits:
##       ptratio < 19.95    to the right, agree=0.895, adj=0.676, (0 split)
##       indus   < 14.345   to the right, agree=0.868, adj=0.595, (0 split)
##       nox     < 0.5825   to the right, agree=0.868, adj=0.595, (0 split)
##       tax     < 397      to the right, agree=0.868, adj=0.595, (0 split)
##       rad     < 16       to the right, agree=0.860, adj=0.568, (0 split)
## 
## Node number 5: 172 observations,    complexity param=0.03672387
##   mean=23.16395, MSE=23.11579 
##   left son=10 (82 obs) right son=11 (90 obs)
##   Primary splits:
##       lstat   < 9.645    to the right, improve=0.24693150, (0 missing)
##       rm      < 6.543    to the left,  improve=0.17749260, (0 missing)
##       ptratio < 17.85    to the right, improve=0.07815189, (0 missing)
##       nox     < 0.5125   to the right, improve=0.07760816, (0 missing)
##       tax     < 267.5    to the right, improve=0.07238020, (0 missing)
##   Surrogate splits:
##       nox   < 0.5125   to the right, agree=0.756, adj=0.488, (0 split)
##       indus < 7.625    to the right, agree=0.750, adj=0.476, (0 split)
##       rm    < 6.26     to the left,  agree=0.738, adj=0.451, (0 split)
##       age   < 65.25    to the right, agree=0.727, adj=0.427, (0 split)
##       dis   < 3.8824   to the left,  agree=0.709, adj=0.390, (0 split)
## 
## Node number 6: 34 observations
##   mean=33.15882, MSE=13.41419 
## 
## Node number 7: 17 observations
##   mean=46.44706, MSE=18.85661 
## 
## Node number 8: 77 observations,    complexity param=0.0110349
##   mean=13.33247, MSE=15.64998 
##   left son=16 (37 obs) right son=17 (40 obs)
##   Primary splits:
##       lstat < 20.1     to the right, improve=0.24481010, (0 missing)
##       crim  < 15.718   to the right, improve=0.23250740, (0 missing)
##       dis   < 2.0037   to the left,  improve=0.17113480, (0 missing)
##       nox   < 0.6615   to the right, improve=0.11757680, (0 missing)
##       rm    < 5.5675   to the left,  improve=0.09054612, (0 missing)
##   Surrogate splits:
##       dis   < 1.9733   to the left,  agree=0.792, adj=0.568, (0 split)
##       rm    < 5.632    to the left,  agree=0.727, adj=0.432, (0 split)
##       age   < 95.35    to the right, agree=0.675, adj=0.324, (0 split)
##       crim  < 9.08499  to the right, agree=0.662, adj=0.297, (0 split)
##       black < 396.295  to the right, agree=0.623, adj=0.216, (0 split)
## 
## Node number 9: 37 observations
##   mean=19.4973, MSE=8.034858 
## 
## Node number 10: 82 observations
##   mean=20.66098, MSE=6.55677 
## 
## Node number 11: 90 observations,    complexity param=0.01695185
##   mean=25.44444, MSE=27.29425 
##   left son=22 (83 obs) right son=23 (7 obs)
##   Primary splits:
##       age   < 86.7     to the left,  improve=0.1844883, (0 missing)
##       lstat < 4.46     to the right, improve=0.1773076, (0 missing)
##       dis   < 3.0037   to the right, improve=0.1652768, (0 missing)
##       crim  < 0.628575 to the left,  improve=0.1203635, (0 missing)
##       nox   < 0.5585   to the left,  improve=0.1122403, (0 missing)
##   Surrogate splits:
##       nox     < 0.5585   to the left,  agree=0.978, adj=0.714, (0 split)
##       dis     < 2.1491   to the right, agree=0.978, adj=0.714, (0 split)
##       crim    < 0.643205 to the left,  agree=0.967, adj=0.571, (0 split)
##       indus   < 16.57    to the left,  agree=0.956, adj=0.429, (0 split)
##       ptratio < 14.75    to the right, agree=0.956, adj=0.429, (0 split)
## 
## Node number 16: 37 observations
##   mean=11.2973, MSE=10.14026 
## 
## Node number 17: 40 observations
##   mean=15.215, MSE=13.37128 
## 
## Node number 22: 83 observations,    complexity param=0.01422576
##   mean=24.79277, MSE=13.56694 
##   left son=44 (55 obs) right son=45 (28 obs)
##   Primary splits:
##       rm      < 6.543    to the left,  improve=0.3377388, (0 missing)
##       lstat   < 5.41     to the right, improve=0.2548210, (0 missing)
##       tax     < 267.5    to the right, improve=0.2210129, (0 missing)
##       ptratio < 18.05    to the right, improve=0.1394682, (0 missing)
##       dis     < 6.4889   to the right, improve=0.1125739, (0 missing)
##   Surrogate splits:
##       lstat   < 5.055    to the right, agree=0.783, adj=0.357, (0 split)
##       ptratio < 15.75    to the right, agree=0.723, adj=0.179, (0 split)
##       crim    < 0.39646  to the left,  agree=0.699, adj=0.107, (0 split)
##       chas    < 0.5      to the left,  agree=0.687, adj=0.071, (0 split)
##       age     < 74.15    to the left,  agree=0.687, adj=0.071, (0 split)
## 
## Node number 23: 7 observations
##   mean=33.17143, MSE=125.3192 
## 
## Node number 44: 55 observations
##   mean=23.26545, MSE=8.880443 
## 
## Node number 45: 28 observations
##   mean=27.79286, MSE=9.189949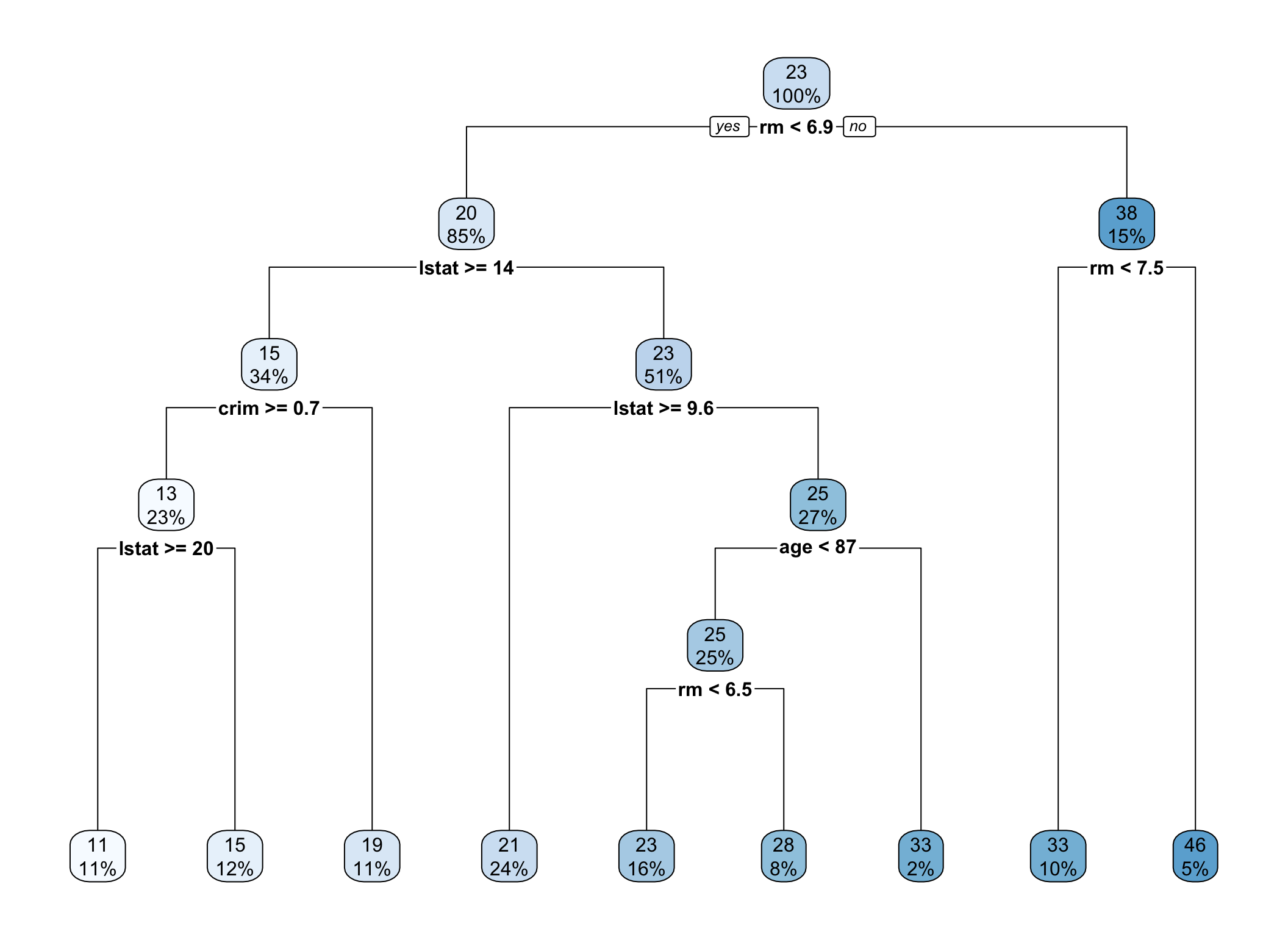
rpart.plot(boston.rpart)
Drzewo regresyjne pełne

Rysunek 5.1: Drzewo regresyjne pełne

Przycinamy drzewo…

printcp(boston.rpart)
## 
## Regression tree:
## rpart(formula = medv ~ ., data = boston.train)
## 
## Variables actually used in tree construction:
## [1] age   crim  lstat rm   
## 
## Root node error: 26734/337 = 79.33
## 
## n= 337 
## 
##         CP nsplit rel error  xerror     xstd
## 1 0.498398      0   1.00000 1.00869 0.102595
## 2 0.157251      1   0.50160 0.54429 0.061257
## 3 0.074856      2   0.34435 0.40320 0.051393
## 4 0.036724      3   0.26949 0.31278 0.045992
## 5 0.035527      4   0.23277 0.29745 0.045608
## 6 0.016952      5   0.19724 0.25532 0.040230
## 7 0.014226      6   0.18029 0.27138 0.040991
## 8 0.011035      7   0.16607 0.27448 0.041078
## 9 0.010000      8   0.15503 0.27204 0.041193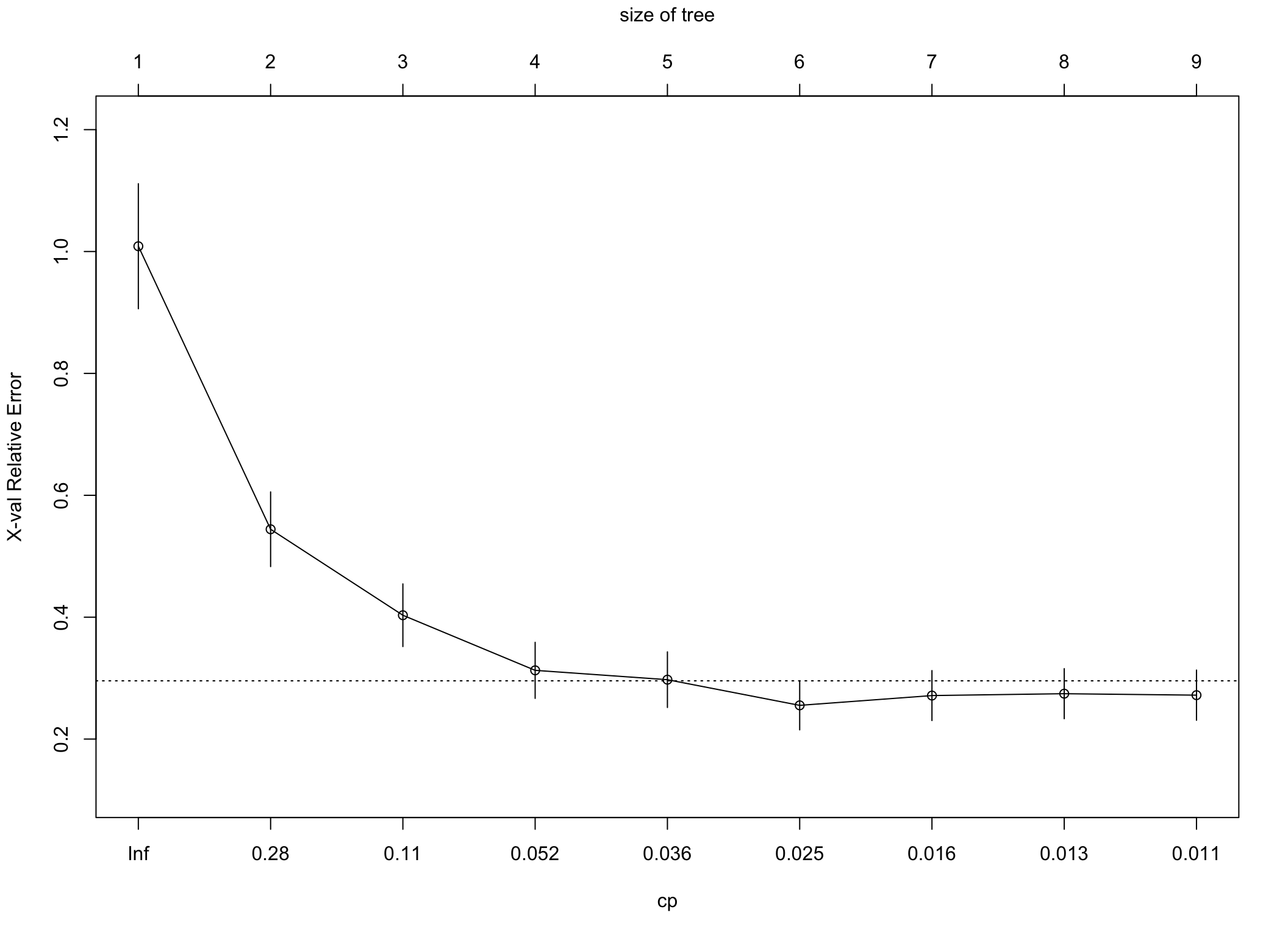
plotcp(boston.rpart)

boston.rpart2 <- prune(boston.rpart, cp = 0.016952)
rpart.plot(boston.rpart2)
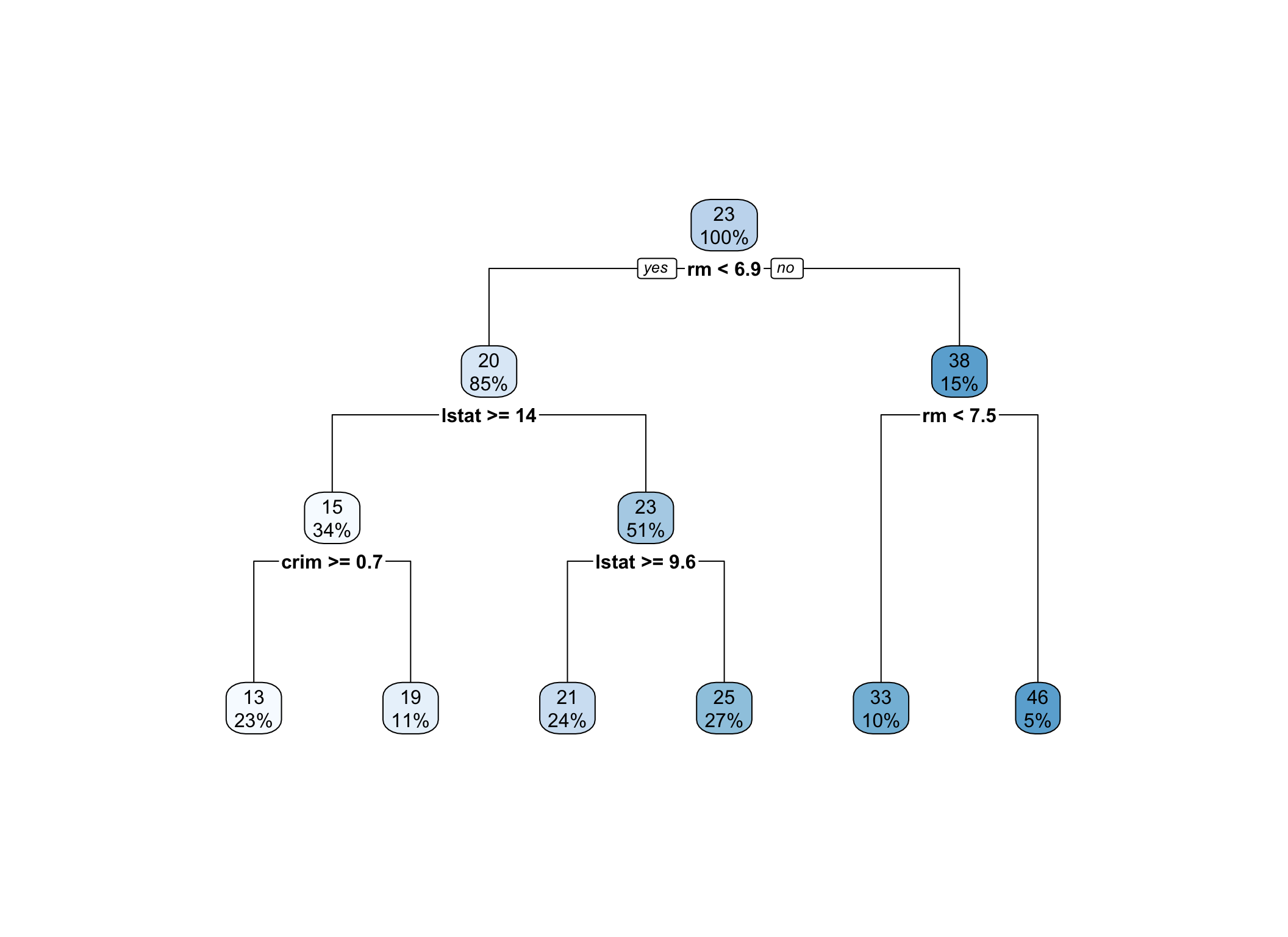
Drzewo regresyjne przycięte

Rysunek 5.2: Drzewo regresyjne przycięte

Predykcja na podstawie drzewa na zbiorze testowym.

boston.pred <- predict(boston.rpart2, newdata = boston.test)
rmse <- function(pred, obs) sqrt(1/length(pred)*sum((pred-obs)^2))
rmse(boston.pred, boston.test$medv)
## [1] 5.830722

Teraz zbudujemy model metodą bagging.

library(randomForest)
boston.bag <- randomForest(medv~., data = boston.train, 
                           mtry = ncol(boston.train)-1)
boston.bag
## 
## Call:
##  randomForest(formula = medv ~ ., data = boston.train, mtry = ncol(boston.train) -      1) 
##                Type of random forest: regression
##                      Number of trees: 500
## No. of variables tried at each split: 13
## 
##           Mean of squared residuals: 12.03374
##                     % Var explained: 84.83

Predykcja na podstawie modelu

boston.pred2 <- predict(boston.bag, newdata = boston.test)
rmse(boston.pred2, boston.test$medv)
## [1] 4.359119

Zatem predykcja na podstawie modelu bagging jest nico lepsza niż z pojedynczego drzewa. Dodatkowo możemy ocenić ważność zmiennych użytych w budowie drzew.

varImpPlot(boston.bag)
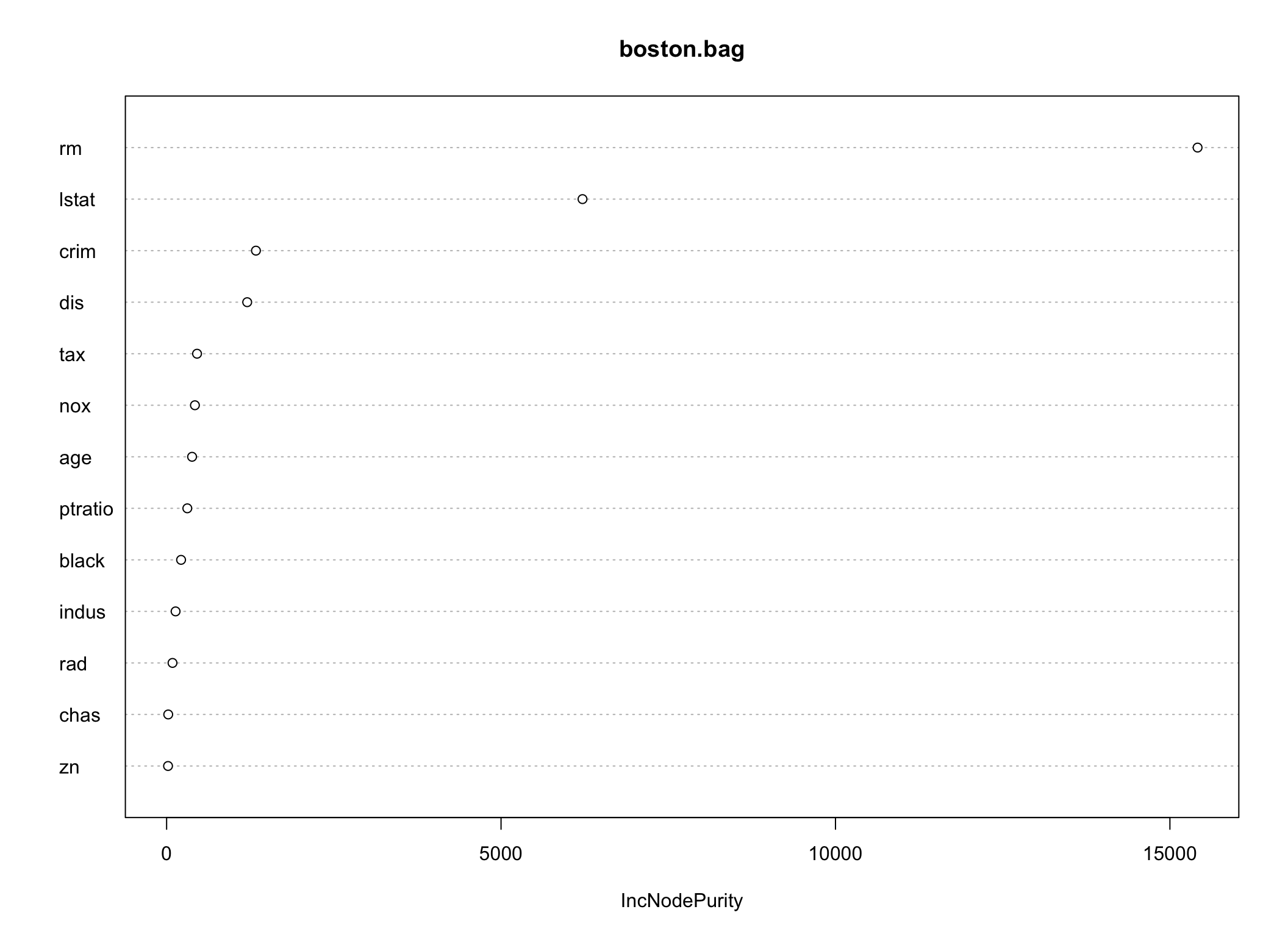
Wykres ważności predyktorów

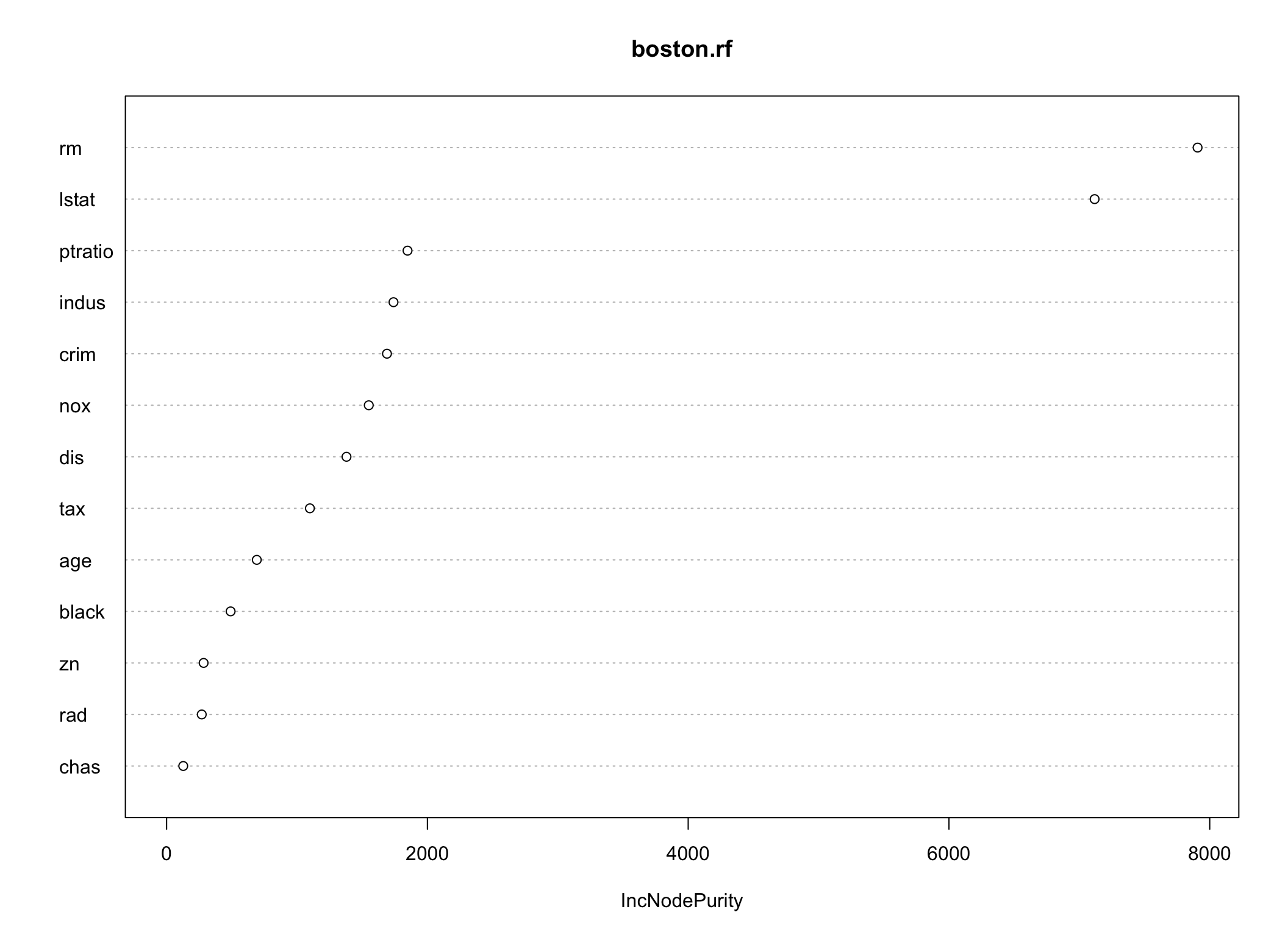
Rysunek 5.3: Wykres ważności predyktorów 

importance(boston.bag)
##         IncNodePurity
## crim       1335.62584
## zn           21.35274
## indus       134.28748
## chas         24.07230
## nox         423.26229
## rm        15413.69291
## age         380.78172
## dis        1204.86690
## rad          88.28151
## tax         454.99800
## ptratio     309.58412
## black       216.15512
## lstat      6217.95834
x$variable.importance
##          rm       lstat       indus     ptratio        crim         age 
## 16276.30598  9170.91941  4427.10554  4039.00112  3412.53062  3170.82658 
##         nox         dis          zn         tax         rad        chas 
##  3063.70694  2681.24858  1306.29569   800.17910   539.07271   262.60146 
##       black 
##    63.78554

W porównaniu do ważności zmiennych dla pojedynczego drzewa widać pewne różnice.

5.2 Lasy losowe

Lasy losowe są uogólnieniem metody bagging, polegającą na losowaniu dla każdego drzewa wchodzącego w skład lasu \(m\) predyktorów spośród \(p\) dostępnych, a następnie budowaniu drzew z wykorzystaniem tylko tych predyktorów (Ho 1995). Dzięki temu za każdy razem drzewo jest budowane w oparciu o nowy zestaw cech (najczęściej przyjmujemy \(m=\sqrt{p}\)). W przypadku modeli bagging za każdym razem najsilniejszy predyktor wchodził w skład zbioru uczącego, a co za tym idzie również uczestniczył w tworzeniu reguł podziału. Wówczas wiele drzew zawierało reguły stosujące dany atrybut, a wtedy predykcje otrzymywane za pomocą drzew były skorelowane. Dlatego nawet duża liczba prób bootstrapowych nie zapewniała poprawy precyzji. Implementacja tej metody znajduje się w pakiecie randomForest.

Przykład 5.2 Kontynuując poprzedni przykład 5.1 możemy zbudować las losowy aby przekonać się czy nastąpi poprawa predykcji zmiennej wynikowej.

boston.rf <- randomForest(medv~., data = boston.train)
boston.rf
## 
## Call:
##  randomForest(formula = medv ~ ., data = boston.train) 
##                Type of random forest: regression
##                      Number of trees: 500
## No. of variables tried at each split: 4
## 
##           Mean of squared residuals: 12.05123
##                     % Var explained: 84.81

Porównanie MSE na próbach uczących pomiędzy lasem losowym i modelem bagging wypada nieco na korzyść bagging.

boston.pred3 <- predict(boston.rf, newdata = boston.test)
rmse(boston.pred3, boston.test$medv)
## [1] 3.79973

Ważność zmiennych również się nieco różni.

varImpPlot(boston.rf)

5.3 Boosting

Rozważania na temat metody boosting zaczęły się od pytań postawionych w publikacji Kearns and Valiant (1989), czy da się na podstawie na podstawie zbioru słabych modeli stworzyć jeden dobry? Odpowiedzi pozytywnej na nie udzielili, najpierw Schapire (1990), a potem Breiman (1998). W metodzie boosting nie stosuje się prób bootstrapowych ale odpowiednio modyfikuje się drzewo wyjściowe w kolejnych krokach na tym samym zbiorze uczącym. Algorytm dla drzewa regresyjnego jest następujący:

  1. Ustal \(\hat{f}(x)=0\) i \(r_i=y_i\) dla każdego \(i\) w zbiorze uczącym.
  2. Dla \(b=1,2,\ldots, B\) powtarzaj:
    1. naucz drzewo \(\hat{f}^b\) o \(d\) regułach podziału (czyli \(d+1\) liściach) na zbiorze \((X_i, r_i)\),
    2. zaktualizuj drzewo do nowej “skurczonej” wersji \[\begin{equation} \hat{f}(x)\leftarrow \hat{f}(x)+\lambda\hat{f}^b(x), \end{equation}\]
    3. zaktualizuj reszty \[\begin{equation} r_i\leftarrow r_i-\lambda\hat{f}^b(x_i). \end{equation}\]
  3. Wyznacz boosted model \[\begin{equation} \hat{f}(x) = \sum_{b=1}^B\lambda\hat{f}^b(x) \end{equation}\]

Uczenie drzew klasyfikacyjnego metoda boosting przebiega w podobny sposób. Wynik uczenia drzew metodą boosting zależy od trzech parametrów:

  1. Liczby drzew \(B\). W przeciwieństwie do metody bagging i lasów losowych, zbyt duże \(B\) może doprowadzić do przeuczenia modelu. \(B\) ustala się najczęściej na podstawie walidacji krzyżowej.
  2. Parametru “kurczenia” (ang. shrinkage) \(\lambda\). Kontroluje on szybkość uczenia się kolejnych drzew. Typowe wartości \(\lambda\) to 0.01 lub 0.001. Bardzo małe \(\lambda\) może wymagać dobrania większego \(B\), aby zapewnić dobrą jakość predykcyjną modelu.
  3. Liczby podziałów w drzewach \(d\), która decyduje o złożoności drzewa. Bywa, że nawet \(d=1\) daje dobre rezultaty, ponieważ model wówczas uczy się powoli.

Implementację metody boosting można znaleźć w pakiecie gbm (Greenwell et al. 2019)

Przykład 5.3 Metodę boosting zastosujemy do zadania predykcji ceny mieszkań na przedmieściach Bostonu. Dobór parametrów modelu będzie arbitralny, więc niekoniecznie model będzie najlepiej dopasowany.

library(gbm)
boston.boost <- gbm(medv~., data = boston.train,
                    distribution = "gaussian", 
                    n.trees = 5000,
                    interaction.depth = 2,
                    shrinkage = 0.01)
boston.boost
## gbm(formula = medv ~ ., distribution = "gaussian", data = boston.train, 
##     n.trees = 5000, interaction.depth = 2, shrinkage = 0.01)
## A gradient boosted model with gaussian loss function.
## 5000 iterations were performed.
## There were 13 predictors of which 13 had non-zero influence.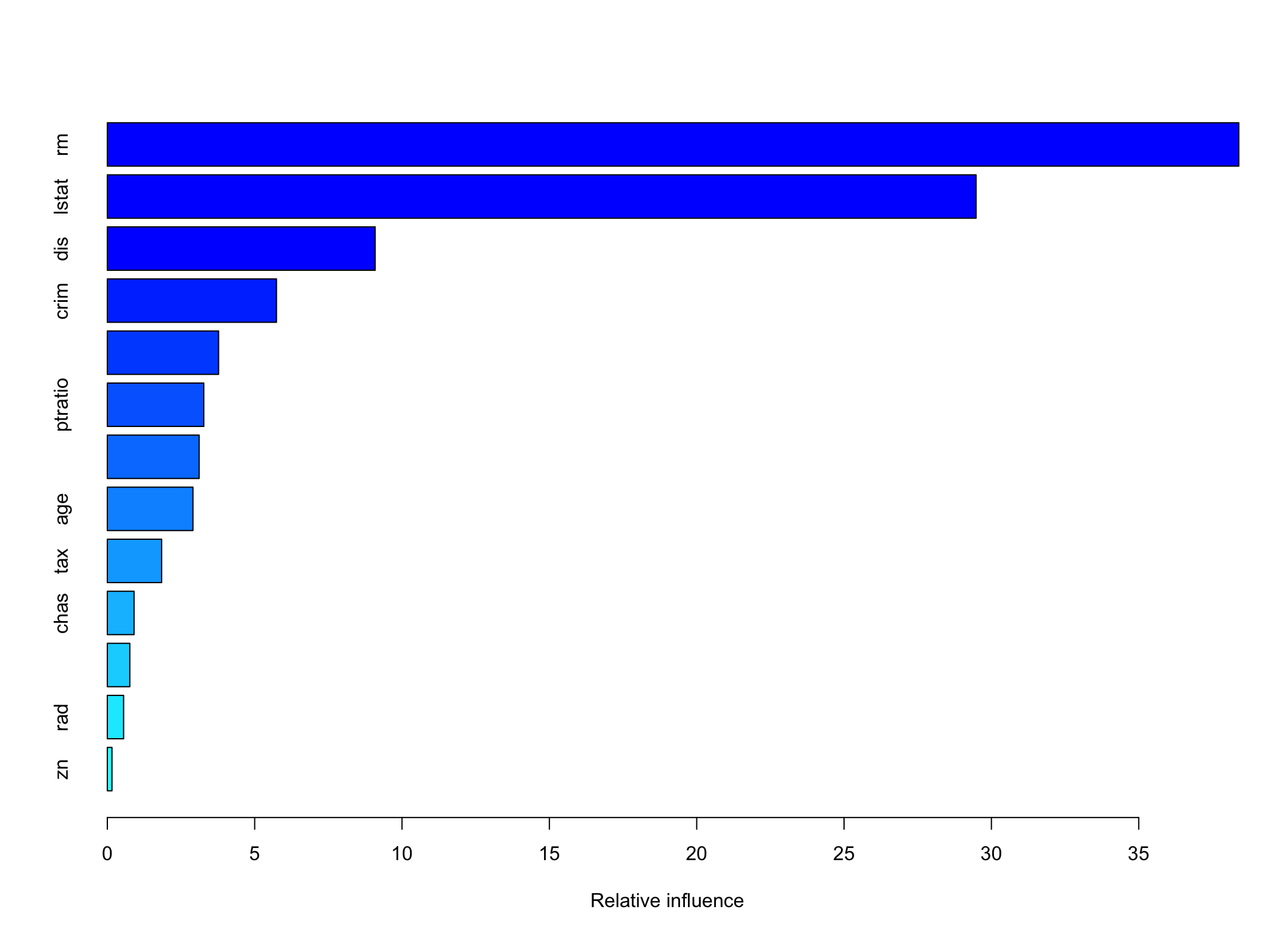
summary(boston.boost)

##             var    rel.inf
## rm           rm 38.3955886
## lstat     lstat 29.4805422
## dis         dis  9.0886721
## crim       crim  5.7399540
## nox         nox  3.7754214
## ptratio ptratio  3.2740541
## black     black  3.1164954
## age         age  2.9063950
## tax         tax  1.8433918
## chas       chas  0.9067974
## indus     indus  0.7627923
## rad         rad  0.5523485
## zn           zn  0.1575472

Predykcja na podstawie metody boosting

boston.pred4 <- predict(boston.boost, newdata = boston.test, n.trees = 5000)
rmse(boston.pred4, boston.test$medv)
## [1] 3.801233

\(RMSE\) jest w tym przypadku nieco większe niż w lasach losowych ale sporo mniejsze niż w metodzie bagging. Wszystkie metody wzmacnianych drzew dają wyniki lepsze niż pojedyncze drzewa.

Bibliografia

Breiman, Leo. 1996. “Bagging Predictors.” Machine Learning 24 (2): 123–40. https://doi.org/10.1007/BF00058655.
———. 1998. “Arcing Classifier (with Discussion and a Rejoinder by the Author).” Ann. Statist. 26 (3): 801–49. https://doi.org/10.1214/aos/1024691079.
Greenwell, Brandon, Bradley Boehmke, Jay Cunningham, and GBM Developers. 2019. Gbm: Generalized Boosted Regression Models. https://CRAN.R-project.org/package=gbm.
Ho, Tin Kam. 1995. “Random Decision Forests.” In Proceedings of 3rd International Conference on Document Analysis and Recognition, 1:278–82. IEEE.
Kearns, M., and L. G. Valiant. 1989. “Crytographic Limitations on Learning Boolean Formulae and Finite Automata.” Annual ACM Symposium on Theory of Computing, 433. http://search.ebscohost.com/login.aspx?direct=true&db=edb&AN=73725380&lang=pl&site=eds-live&scope=site.
Liaw, Andy, and Matthew Wiener. 2002. “Classification and Regression by randomForest.” R News 2 (3): 18–22. https://CRAN.R-project.org/doc/Rnews/.
Peters, Andrea, and Torsten Hothorn. 2018. Ipred: Improved Predictors. https://CRAN.R-project.org/package=ipred.
Schapire, Robert E. 1990. “The Strength of Weak Learnability.” Machine Learning 5 (2): 197–227. https://doi.org/10.1007/BF00116037.
Venables, W. N., and B. D. Ripley. 2002. Modern Applied Statistics with s. Fourth. New York: Springer. http://www.stats.ox.ac.uk/pub/MASS4.

  1. chyba tylko dla drugiej metody istniej dobre polskie tłumaczenie nazwy - las losowy↩︎