2 Przygotowanie danych

Dane, które importujemy z zewnętrznego źródła najczęściej nie spełniają formatów obowiązujących w R. Często zmienne zawierają niedopuszczalne znaki szczególne, odstępy w nazwach, powtórzone nazwy kolumn, nazwy zmiennych zaczynające się od liczby, czy puste wiersze lub kolumny. Przed przystąpieniem do analizy zbioru należy rozważyć ewentualne poprawki nazw zmiennych, czy usunięcie pustych kolumn i wierszy. Niektórych czynności można dokonać już na etapie importu danych, stosując pewne pakiety oraz nowe funkcjonalności środowiska RStudio. W większości przypadków uchroni nas to od żmudnego przekształcania typów zmiennych. Oczywiście wszystkie te czynności czyszczenia danych można również dokonać już po imporcie danych, za pomocą odpowiednich komend R.

## przykładowe niepożądane nazwy zmiennych
test_df <- as.data.frame(matrix(rnorm(18),ncol = 6))
names(test_df) <- c("hIgHlo", "REPEAT VALUE", "REPEAT VALUE",
                    "% successful (2009)",  "abc@!*", "")
test_df
##       hIgHlo REPEAT VALUE REPEAT VALUE % successful (2009)     abc@!*
## 1  0.6168258    0.2199210    0.7472476         -0.01442705 -1.0376863
## 2 -1.6412652   -0.3723289    0.6567005          1.16991530  0.8756566
## 3  0.6354212    0.7113021   -0.5793268          0.10611187  0.5580122
##             
## 1 -0.6409736
## 2  0.3027098
## 3 -0.8205682
## do poprawy nazw zmiennych użyjemy funkcji make.names
names(test_df) <- make.names(names(test_df))
test_df
##       hIgHlo REPEAT.VALUE REPEAT.VALUE X..successful..2009.     abc...
## 1  0.6168258    0.2199210    0.7472476          -0.01442705 -1.0376863
## 2 -1.6412652   -0.3723289    0.6567005           1.16991530  0.8756566
## 3  0.6354212    0.7113021   -0.5793268           0.10611187  0.5580122
##            X
## 1 -0.6409736
## 2  0.3027098
## 3 -0.8205682

Efekt końcowy choć skuteczny, to nie jest zadowalający. Czyszczenia nazw zmiennych można też dokonać stosując funkcję clean_names pakietu janitor (Firke 2018). Pozwala on również na usuwanie pustych wierszy i kolumn, znajdowanie zduplikowanych rekordów, itp.

library(janitor)
test_df %>% # aby na stałe zmienić nazwy zmiennych trzeba podstawienia
    clean_names()
##     h_ig_hlo repeat_value repeat_value_2 x_successful_2009        abc
## 1  0.6168258    0.2199210      0.7472476       -0.01442705 -1.0376863
## 2 -1.6412652   -0.3723289      0.6567005        1.16991530  0.8756566
## 3  0.6354212    0.7113021     -0.5793268        0.10611187  0.5580122
##            x
## 1 -0.6409736
## 2  0.3027098
## 3 -0.8205682
# przykładowe dane
x <- data.frame(w1=c(1,4,2,NA),w2=c(NA,2,3,NA), w3=c(1,NA,1,NA))
x
##   w1 w2 w3
## 1  1 NA  1
## 2  4  2 NA
## 3  2  3  1
## 4 NA NA NA
x %>% remove_empty("rows")
##   w1 w2 w3
## 1  1 NA  1
## 2  4  2 NA
## 3  2  3  1

2.1 Identyfikacja braków danych

Zanim usuniemy jakiekolwiek braki w zbiorze, powinniśmy je najpierw zidentyfikować, określić ich charakter, a dopiero potem ewentualnie podjąć decyzję o uzupełnianiu braków.

algae <- rio::import("data/algae.csv")

# najprościej jest wywołać summary
summary(algae)
##     season              size              speed                mxPH      
##  Length:200         Length:200         Length:200         Min.   :5.600  
##  Class :character   Class :character   Class :character   1st Qu.:7.700  
##  Mode  :character   Mode  :character   Mode  :character   Median :8.060  
##                                                           Mean   :8.012  
##                                                           3rd Qu.:8.400  
##                                                           Max.   :9.700  
##                                                           NA's   :1      
##       mnO2              Cl               NO3              NH4          
##  Min.   : 1.500   Min.   :  0.222   Min.   : 0.050   Min.   :    5.00  
##  1st Qu.: 7.725   1st Qu.: 10.981   1st Qu.: 1.296   1st Qu.:   38.33  
##  Median : 9.800   Median : 32.730   Median : 2.675   Median :  103.17  
##  Mean   : 9.118   Mean   : 43.636   Mean   : 3.282   Mean   :  501.30  
##  3rd Qu.:10.800   3rd Qu.: 57.824   3rd Qu.: 4.446   3rd Qu.:  226.95  
##  Max.   :13.400   Max.   :391.500   Max.   :45.650   Max.   :24064.00  
##  NA's   :2        NA's   :10        NA's   :2        NA's   :2         
##       oPO4             PO4              Chla               a1       
##  Min.   :  1.00   Min.   :  1.00   Min.   :  0.200   Min.   : 0.00  
##  1st Qu.: 15.70   1st Qu.: 41.38   1st Qu.:  2.000   1st Qu.: 1.50  
##  Median : 40.15   Median :103.29   Median :  5.475   Median : 6.95  
##  Mean   : 73.59   Mean   :137.88   Mean   : 13.971   Mean   :16.92  
##  3rd Qu.: 99.33   3rd Qu.:213.75   3rd Qu.: 18.308   3rd Qu.:24.80  
##  Max.   :564.60   Max.   :771.60   Max.   :110.456   Max.   :89.80  
##  NA's   :2        NA's   :2        NA's   :12                       
##        a2               a3               a4               a5        
##  Min.   : 0.000   Min.   : 0.000   Min.   : 0.000   Min.   : 0.000  
##  1st Qu.: 0.000   1st Qu.: 0.000   1st Qu.: 0.000   1st Qu.: 0.000  
##  Median : 3.000   Median : 1.550   Median : 0.000   Median : 1.900  
##  Mean   : 7.458   Mean   : 4.309   Mean   : 1.992   Mean   : 5.064  
##  3rd Qu.:11.375   3rd Qu.: 4.925   3rd Qu.: 2.400   3rd Qu.: 7.500  
##  Max.   :72.600   Max.   :42.800   Max.   :44.600   Max.   :44.400  
##                                                                     
##        a6               a7        
##  Min.   : 0.000   Min.   : 0.000  
##  1st Qu.: 0.000   1st Qu.: 0.000  
##  Median : 0.000   Median : 1.000  
##  Mean   : 5.964   Mean   : 2.495  
##  3rd Qu.: 6.925   3rd Qu.: 2.400  
##  Max.   :77.600   Max.   :31.600  
## 
## wyświetl niekompletne wiersze
algae[!complete.cases(algae),] %>% head()
##    season  size  speed mxPH mnO2   Cl   NO3 NH4 oPO4 PO4 Chla   a1  a2  a3   a4
## 28 autumn small   high  6.8 11.1 9.00 0.630  20  4.0  NA  2.7 30.3 1.9 0.0  0.0
## 38 spring small   high  8.0   NA 1.45 0.810  10  2.5 3.0  0.3 75.8 0.0 0.0  0.0
## 48 winter small    low   NA 12.6 9.00 0.230  10  5.0 6.0  1.1 35.5 0.0 0.0  0.0
## 55 winter small   high  6.6 10.8   NA 3.245  10  1.0 6.5   NA 24.3 0.0 0.0  0.0
## 56 spring small medium  5.6 11.8   NA 2.220   5  1.0 1.0   NA 82.7 0.0 0.0  0.0
## 57 autumn small medium  5.7 10.8   NA 2.550  10  1.0 4.0   NA 16.8 4.6 3.9 11.5
##     a5  a6  a7
## 28 2.1 1.4 2.1
## 38 0.0 0.0 0.0
## 48 0.0 0.0 0.0
## 55 0.0 0.0 0.0
## 56 0.0 0.0 0.0
## 57 0.0 0.0 0.0
## policz niekompletne wiersze
nrow(algae[!complete.cases(algae),])
## [1] 16
## sprawdzenie liczby braków w wierszach
apply(algae, 1, function(x) sum(is.na(x)))
##   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18  19  20 
##   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0 
##  21  22  23  24  25  26  27  28  29  30  31  32  33  34  35  36  37  38  39  40 
##   0   0   0   0   0   0   0   1   0   0   0   0   0   0   0   0   0   1   0   0 
##  41  42  43  44  45  46  47  48  49  50  51  52  53  54  55  56  57  58  59  60 
##   0   0   0   0   0   0   0   1   0   0   0   0   0   0   2   2   2   2   2   2 
##  61  62  63  64  65  66  67  68  69  70  71  72  73  74  75  76  77  78  79  80 
##   2   6   1   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0 
##  81  82  83  84  85  86  87  88  89  90  91  92  93  94  95  96  97  98  99 100 
##   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0 
## 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 
##   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   1   0   0   0   0 
## 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 
##   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0 
## 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 
##   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0 
## 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 
##   1   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0 
## 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 
##   0   0   0   1   0   0   0   0   0   0   0   0   0   0   0   0   0   0   6   0

Wiele ciekawych funkcji do eksploracji danych znajduje się w pakiecie DMwR (Torgo 2013), który został przygotowany przy okazji publikacji książki Data Mining with R.

## poszukiwanie wierszy zawierających wiele braków
## w tym przypadku próg wyświetlania ustawiony jest na 0.2
## czyli 20% wszystkich kolumn
library(DMwR2)
manyNAs(algae)
##  62 199 
##  62 199
## tworzenie zbioru pozbawionego wierszy zawierających wiele braków
algae2 <- algae[-manyNAs(algae), ]

## sprawdzamy liczbę wybrakowanych wierszy które pozostały
nrow(algae2[!complete.cases(algae2),])
## [1] 14
## usuwamy wszystkie wiersze z brakami
algae3 <- na.omit(algae)
    
## wyświetl wiersze z brakami
algae3[!complete.cases(algae3),] %>% head()
##  [1] season size   speed  mxPH   mnO2   Cl     NO3    NH4    oPO4   PO4   
## [11] Chla   a1     a2     a3     a4     a5     a6     a7    
## <0 rows> (or 0-length row.names)
## liczba pozostałych wybrakowanych wierszy
nrow(algae3[!complete.cases(algae3),])
## [1] 0
## można oczywiście też ręcznie usuwać wiersze (nie polecam)
algae4 <- algae[-c(62,199),]

Można też zbudować funkcję, która będzie usuwała braki danych wg naszego upodobania.

## najpierw budujemy funkcję i ją kompilujemy aby R mógł ja stosować
## parametr prog ustala próg odcięcia wierszy
czysc.dane <- function(dt, prog = 0){
    licz.braki <- apply(dt, 1, function(x) sum(is.na(x)))
    czyste.dt <- dt[!(licz.braki/ncol(dt)>prog), ]
    return(czyste.dt)
}
    
## potem ją możemy stosować
algae4 <- czysc.dane(algae)
nrow(algae4[!complete.cases(algae4),])
## [1] 0
## czyścimy wiersze, których liczba braków przekracza 20% wszystkich kolumn
algae5 <- czysc.dane(algae, prog = 0.2)
nrow(algae5[!complete.cases(algae5),])
## [1] 14

Bardzo ciekawym narzędziem do znajdowania braków danych jest funkcja md.pattern pakietu mice (van Buuren and Groothuis-Oudshoorn 2018). Wskazuje on ile braków występuje w ramach każdej zmiennej.

library(mice)
md.pattern(algae)
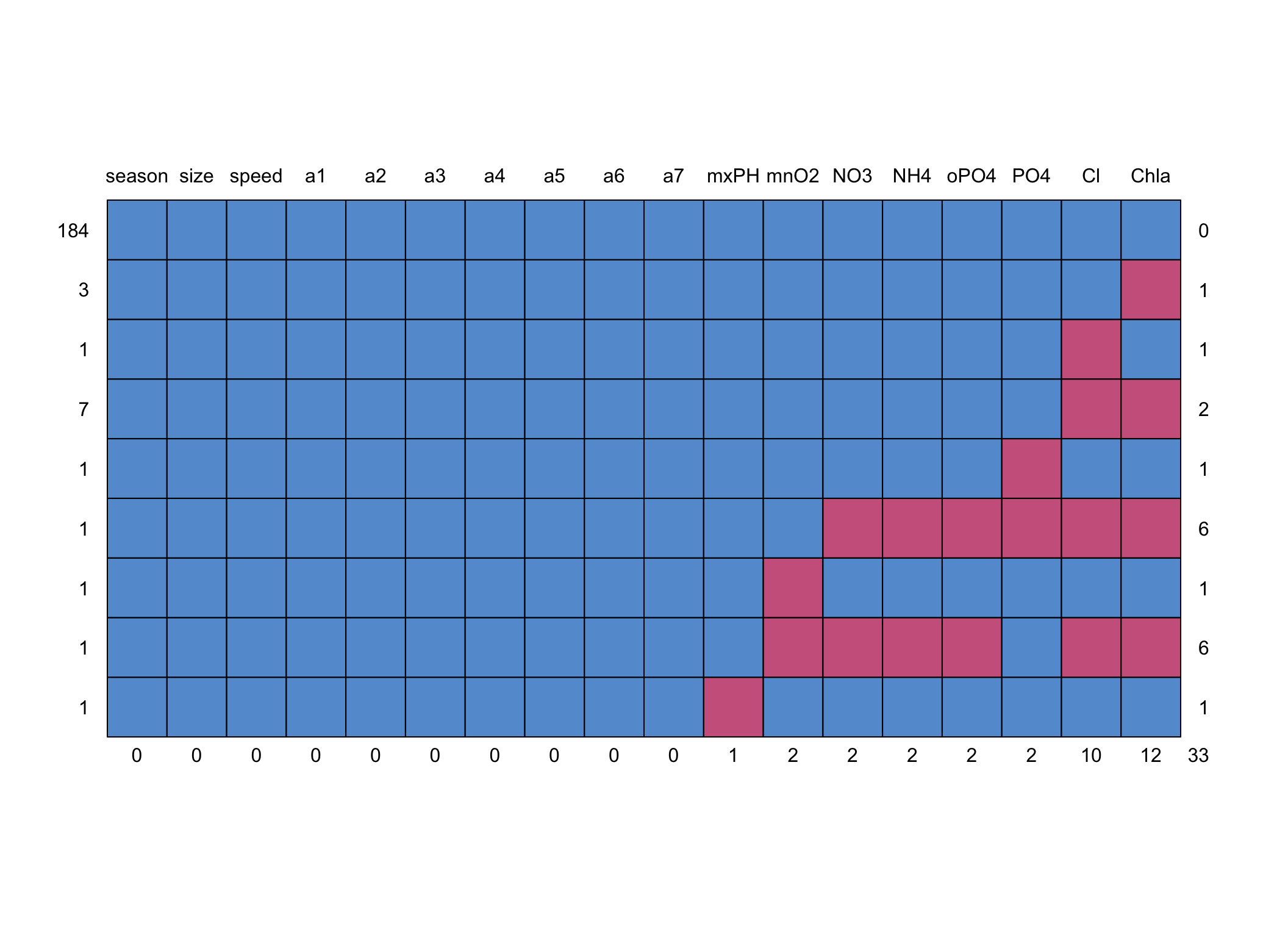
Na czerwono zaznaczone są zmienne, które zwierają braki danych. Liczba w wierszu po lewej stronie wykresu wskazuje ile wierszy w bazie ma daną charakterystykę, a liczba po prawej oznacza ile zmiennych było *wybrakowanych*

Rysunek 2.1: Na czerwono zaznaczone są zmienne, które zwierają braki danych. Liczba w wierszu po lewej stronie wykresu wskazuje ile wierszy w bazie ma daną charakterystykę, a liczba po prawej oznacza ile zmiennych było wybrakowanych 

##     season size speed a1 a2 a3 a4 a5 a6 a7 mxPH mnO2 NO3 NH4 oPO4 PO4 Cl Chla
## 184      1    1     1  1  1  1  1  1  1  1    1    1   1   1    1   1  1    1
## 3        1    1     1  1  1  1  1  1  1  1    1    1   1   1    1   1  1    0
## 1        1    1     1  1  1  1  1  1  1  1    1    1   1   1    1   1  0    1
## 7        1    1     1  1  1  1  1  1  1  1    1    1   1   1    1   1  0    0
## 1        1    1     1  1  1  1  1  1  1  1    1    1   1   1    1   0  1    1
## 1        1    1     1  1  1  1  1  1  1  1    1    1   0   0    0   0  0    0
## 1        1    1     1  1  1  1  1  1  1  1    1    0   1   1    1   1  1    1
## 1        1    1     1  1  1  1  1  1  1  1    1    0   0   0    0   1  0    0
## 1        1    1     1  1  1  1  1  1  1  1    0    1   1   1    1   1  1    1
##          0    0     0  0  0  0  0  0  0  0    1    2   2   2    2   2 10   12
##       
## 184  0
## 3    1
## 1    1
## 7    2
## 1    1
## 1    6
## 1    1
## 1    6
## 1    1
##     33

2.2 Zastępowanie braków danych

Zastępowanie braków danych (zwane także imputacją danych) jest kolejnym etapem procesu przygotowania danych do analiz. Nie można jednak wyróżnić uniwersalnego sposobu zastępowania braków dla wszystkich możliwych sytuacji. Wśród statystyków panuje przekonanie, że w przypadku wystąpienia braków danych można zastosować trzy strategie:

  • nic nie robić z brakami - co wydaje się niedorzeczne ale wcale takie nie jest, ponieważ istnieje wiele modeli statystycznych (np. drzewa decyzyjne), które świetnie radzą sobie w sytuacji braków danych. Niestety nie jest to sposób, który można stosować zawsze, ponieważ są również modele wymagające kompletności danych jak na przykład sieci neuronowe.
  • usuwać braki wierszami9 - to metoda, która jest stosowana domyślnie w przypadku kiedy twórca modelu nie zadecyduje o innym sposobie obsługi luk. Metoda ta ma swoją niewątpliwą zaletę w postaci jasnej i prostej procedury, ale szczególnie w przypadku niewielkich zbiorów może skutkować obciążeniem estymatorów. Nie wiemy bowiem jaka wartość faktycznie jest przypisana danej cesze. Jeśli jest to wartość bliska np. średniej, to nie wpłynie znacząco na obciążenie estymatora wartości oczekiwanej. W przypadku, gdy różni się ona znacznie od średniej tej cechy, to estymator może już wykazywać obciążenie. Jego wielkość zależy również od liczby usuniętych elementów. Nie jest zalecane usuwanie wielu wierszy ze zbioru danych i na podstawie okrojonego zbioru wyciąganie wniosków o populacji, ponieważ próba jest wówczas znacząco inna niż populacja. Dodatkowo jeśli estymatory są wyznaczane na podstawie zbioru wyraźnie mniej licznego, to precyzja estymatorów wyrażona wariancją spada. Reasumując, jeśli liczba wierszy z brakującymi danymi jest niewielka w stosunku do całego zbioru, to usuwanie wierszy jest sensownym rozwiązaniem.
  • uzupełnianie braków - to procedura polegająca na zastępowaniu braków różnymi technikami. Jej niewątpliwą zaletą jest fakt posiadania kompletnych danych bez konieczności usuwania wierszy. Niestety wiąże się to również z pewnymi wadami. Zbiór posiadający wiele braków uzupełnianych nawet bardzo wyrafinowanymi metodami może cechować się zaniżoną wariancją poszczególnych cech oraz tzw. przeuczeniem10.
  1. Uzupełnianie średnią - braki w zakresie danej zmiennej uzupełniamy średnią tej zmiennej przypadków uzupełnionych.
algae[is.na(algae$mxPH), ]
##    season  size speed mxPH mnO2 Cl  NO3 NH4 oPO4 PO4 Chla   a1 a2 a3 a4 a5 a6
## 48 winter small   low   NA 12.6  9 0.23  10    5   6  1.1 35.5  0  0  0  0  0
##    a7
## 48  0
m <- mean(algae$mxPH, na.rm = T)
algae[is.na(algae$mxPH), "mxPH"] <- m
algae[is.na(algae$mxPH), ]
##  [1] season size   speed  mxPH   mnO2   Cl     NO3    NH4    oPO4   PO4   
## [11] Chla   a1     a2     a3     a4     a5     a6     a7    
## <0 rows> (or 0-length row.names)
  1. Uzupełnianie medianą - braki w zakresie danej zmiennej uzupełniamy medianą tej zmiennej przypadków uzupełnionych.
algae %>% filter(is.na(Chla)) %>% head
##   season  size  speed mxPH mnO2 Cl   NO3 NH4 oPO4  PO4 Chla   a1  a2  a3   a4
## 1 winter small   high  6.6 10.8 NA 3.245  10    1  6.5   NA 24.3 0.0 0.0  0.0
## 2 spring small medium  5.6 11.8 NA 2.220   5    1  1.0   NA 82.7 0.0 0.0  0.0
## 3 autumn small medium  5.7 10.8 NA 2.550  10    1  4.0   NA 16.8 4.6 3.9 11.5
## 4 spring small   high  6.6  9.5 NA 1.320  20    1  6.0   NA 46.8 0.0 0.0 28.8
## 5 summer small   high  6.6 10.8 NA 2.640  10    2 11.0   NA 46.9 0.0 0.0 13.4
## 6 autumn small medium  6.6 11.3 NA 4.170  10    1  6.0   NA 47.1 0.0 0.0  0.0
##   a5  a6 a7
## 1  0 0.0  0
## 2  0 0.0  0
## 3  0 0.0  0
## 4  0 0.0  0
## 5  0 0.0  0
## 6  0 1.2  0
algae[is.na(algae$Chla), "Chla"] <- median(algae$Chla, na.rm = T)
  1. Wypełnianie zmiennych typu wyliczeniowego, logicznego lub znakowego odbywa się najczęściej przez dobranie w miejsce brakującej wartości, elementu powtarzającego się najczęściej wśród obiektów obserwowanych. W pakiecie DMwR istnieje funkcja centralImputation, która wypełnia braki wartością centralną (w przypadku zmiennych typu liczbowego - medianą, a dla wartości logicznych, wyliczeniowych lub tekstowych - modą).
algae[48, "season"]
## [1] "winter"
algae[48, "season"] <- NA
algae.uzup <- centralImputation(algae)
algae.uzup[48,]
##    season  size speed     mxPH mnO2 Cl  NO3 NH4 oPO4 PO4 Chla   a1 a2 a3 a4 a5
## 48 winter small   low 8.011734 12.6  9 0.23  10    5   6  1.1 35.5  0  0  0  0
##    a6 a7
## 48  0  0
  1. Jeszcze innym sposobem imputacji danych są algorytmy oparte o metodę \(k\)-najbliższych sąsiadów. Algorytm opiera się na prostej zasadzie, uzupełniania brakujących wartości medianą (w przypadku zmiennych ilościowych) lub modą (w przypadku zmiennych jakościowych) elementów, które są \(k\)-tymi najbliższymi sąsiadami w metryce \[\begin{equation}\label{knn} d(x,y)=\sqrt{\sum_{i=1}^{p}\delta_i(x_i,y_i)}, \end{equation}\] gdzie \(\delta_i\) jest odległością pomiędzy dwoma elementami ze względu na \(i\)-tą cech, określoną następująco \[\begin{equation}\label{metryka} \delta_i(v_1, v_2)=\begin{cases} 1,& \text{jeśli zmienna jest jakościowa i }v_1\neq v_2\\ 0,& \text{jeśli zmienna jest jakościowa i }v_1=v_2\\ (v_1-v_2)^2,& \text{jeśli zmienna jest ilościowa.} \end{cases} \end{equation}\] Odległości są mierzone dla zmiennych standaryzowanych. Istnieje też odmiana z wagami, które maleją wraz ze wzrostem odległości pomiędzy sąsiadem a uzupełnianym elementem (np. \(w(d)=\exp(d)\)).
algae[48, ]
##    season  size speed     mxPH mnO2 Cl  NO3 NH4 oPO4 PO4 Chla   a1 a2 a3 a4 a5
## 48   <NA> small   low 8.011734 12.6  9 0.23  10    5   6  1.1 35.5  0  0  0  0
##    a6 a7
## 48  0  0
algae <- algae %>% 
    mutate_if(is.character, as.factor)
algae.uzup <- knnImputation(algae, k = 5, scale = F, meth = "median")
algae.uzup[48,]
##    season  size speed     mxPH mnO2 Cl  NO3 NH4 oPO4 PO4 Chla   a1 a2 a3 a4 a5
## 48 summer small   low 8.011734 12.6  9 0.23  10    5   6  1.1 35.5  0  0  0  0
##    a6 a7
## 48  0  0

Istnieją również dużo bardziej złożone algorytmy imputacji danych oparte na bardziej wyrafinowanych technikach, takich jak: predykcja modelami liniowymi, nieliniowymi, analiza dyskryminacyjna, drzewa klasyfikacyjne. Dwa najbardziej znane pakiety zawierające funkcje do imputacji w sposób złożony, to Amelia i mice.

Imputacja danych z zastosowaniem pakietu mice wymaga podjęcia kilku decyzji przed przystąpieniem do uzupełniania danych:

  1. Czy dane są MAR (ang. Missing At Random) czy MNAR (ang. Missing Not At Random), co oznacza, że musimy się zastanowić jakie mogły być źródła braków danych, przypadkowe czy systematyczne?
  2. Należy się zdecydować na formę imputacji, określając strukturę zależności pomiędzy cechami oraz rozkład błędu danej cechy?
  3. Wybrać zbiór danych, który posłuży nam za predyktory w imputacji (nie mogą zawierać braków).
  4. Określenie, które niepełne zmienne są funkcjami innych wybrakowanych zmiennych.
  5. Określić w jakiej kolejności dane będą imputowane.
  6. Określić parametry startowe imputacji (liczbę iteracji, warunek zbieżności).
  7. Określić liczę imputowanych zbiorów.

Ad 1. Wyróżniamy następujące rodzaje braków danych:

  • MCAR (ang. Missing Completely At Random) - z definicji to braki, których pojawienie się jest kompletnie losowe. Przykładowo gdy osoba poproszona o wypełnienie wieku w ankiecie będzie rzucać monetą czy wypełnić tą zmienną.
  • MAR - oznacza, że obserwowane wartości i wybrakowane mają inne rozkłady ale da się je oszacować na podstawie danych obserwowanych. Przykładowo ciśnienie tętnicze u osób, które nie wypełniły tej wartości jest wyższe niż u osób, które wpisały swoje ciśnienie. Okazuje się, że osoby starsze z nadciśnieniem nie wypełniały ankiety w tym punkcie.
  • MNAR - jeśli nie jest spełniony warunek MCAR i MAR, wówczas brak ma charakter nielosowy. Przykładowo respondenci osiągający wyższe zarobki sukcesywnie nie wypełniają pola “zarobki” i dodatkowo nie ma w ankiecie zmiennych, które pozwoliłyby nam ustalić, jakie to osoby.

Ad 2. Decyzja o algorytmie imputacji wynika bezpośrednio ze skali w jakiej jest mierzona dana zmienna. Ze względu na rodzaj cechy używać będziemy następujących metod:

Tabela 2.1: Zestaw metod imputacji danych stosowanych w pakiecie mice
method type description
pmm any Predictive.mean.matching
midastouch any Weighted predictive mean matching
sample any Random sample from observed values
cart any Classification and regression trees
rf any Random forest imputations
mean numeric Unconditional mean imputation
norm numeric Bayesian linear regression
norm.nob numeric Linear regression ignoring model error
norm.boot numeric Linear regression using bootstrap
norm.predict numeric Linear regression, predicted values
quadratic numeric Imputation of quadratic terms
ri numeric Random indicator for nonignorable data
logreg binary Logistic regression
logreg.boot binary Logistic regression with bootstrap
polr ordered Proportional odds model
polyreg unordered Polytomous logistic regression
lda unordered Linear discriminant analysis
2l.norm numeric Level-1 normal heteroscedastic
2l.lmer numeric Level-1 normal homoscedastic,
lmer
2l.pan numeric Level-1 normal homoscedastic, pan
2l.bin binary Level-1 logistic, glmer
2lonly.mean numeric Level-2 class mean
2lonly.norm numeric Level-2 class normal
2lonly.pmm any Level-2 class predictive mean matching

Każdy z czterech typów danych ma swój domyślny algorytm przeznaczony do imputacji:

  • zmienna ilościowa - pmm
  • zmienna dychotomiczna (stany 0 lub 1) - logreg
  • zmienna typu wyliczeniowego (nieuporządkowana) - polyreg
  • zmienna typu wyliczeniowego (uporządkowana) - polr

Niewątpliwą zaletą metody pmm jest to, że wartości imputowane są ograniczone jedynie do obserwowanych wartości. Metody norm i norm.nob uzupełniają brakujące wartości w oparciu o model liniowy. Są one szybkie i efektywne w przypadku gdy reszty modelu są zbliżone rozkładem do normalności. Druga z tych technik nie bierze pod uwagę niepewności związanej z modelem imputującym. Metoda 2L.norm opiera się na dwupoziomowym heterogenicznym modelu liniowym (skupienia są włączone jako efekt do modelu). Technika polyreg korzysta z funkcji multinom pakietu nnet tworzącej model wielomianowy. polr opiera się o proporcjonalny model logitowy z pakietu MASS. lda to model dyskryminacyjny klasyfikujący obiekty na podstawie prawdopodobieństw a posteriori. Metoda sample zastępuje braki losowa wybranymi wartościami spośród wartości obserwowanych.

Ad 3. Do ustalenia predyktorów w modelu mice służy funkcja predictorMatrix. Po pierwsze wyświetla ona domyślny układ predyktorów włączanych do modelu. Można go dowolnie zmienić i podstawić do modelu imputującego dane parametrem predictorMatrix. Zera występujące w kolejnych wierszach macierzy predyktorów oznaczają pominięcie tej zmiennej przy imputacji innej zmiennej. Jeśli dodatkowo chcemy by jakaś zmienna nie była imputowana, to oprócz usunięcia jej z listy predyktorów, należy wymazać ją z listy metod predykcji (method).

Ogólne zalecenia co do tego jakie zmienne stosować jako predyktory jest takie, żeby brać ich jak najwięcej. Spowoduje to, że bardziej prawdopodobny staje się brak typu MAR a nie MNAR. Z drugiej jednak strony, nierzadko zbiory zawierają olbrzymią liczbę zmiennych i włączanie ich wszystkich do modelu imputującego nie będzie miało sensu.

Zalecenia doboru zmiennych są następujące:

  • weź wszystkie te zmienne, które są włączane do modelu właściwego, czyli tego za pomocą którego chcesz poznać strukturę zależności;
  • czasem do modelu imputującego należy też włączyć interakcje zmiennych z modelu właściwego;
  • dodaj zmienne, które mogą mieć wpływ na wybrakowane cechy;
  • włącz zmienne istotnie podnoszące poziom wyjaśnionej wariancji modelu;
  • na koniec usuń te zmienne spośród predyktorów, które same zawierają zbyt wiele braków.

Ad 4-7. Decyzje podejmowane w tych punktach zależą istotnie od analizowanego zbioru i będą przedmiotem oddzielnych analiz w kontekście rozważanych zbiorów i zadań.

Przykład 2.1 Dokonamy imputacji zbioru airquality z wykorzystaniem pakietów mice i VIM (Templ et al. 2019)

data <- airquality
summary(data)
##      Ozone           Solar.R           Wind             Temp      
##  Min.   :  1.00   Min.   :  7.0   Min.   : 1.700   Min.   :56.00  
##  1st Qu.: 18.00   1st Qu.:115.8   1st Qu.: 7.400   1st Qu.:72.00  
##  Median : 31.50   Median :205.0   Median : 9.700   Median :79.00  
##  Mean   : 42.13   Mean   :185.9   Mean   : 9.958   Mean   :77.88  
##  3rd Qu.: 63.25   3rd Qu.:258.8   3rd Qu.:11.500   3rd Qu.:85.00  
##  Max.   :168.00   Max.   :334.0   Max.   :20.700   Max.   :97.00  
##  NA's   :37       NA's   :7                                       
##      Month            Day      
##  Min.   :5.000   Min.   : 1.0  
##  1st Qu.:6.000   1st Qu.: 8.0  
##  Median :7.000   Median :16.0  
##  Mean   :6.993   Mean   :15.8  
##  3rd Qu.:8.000   3rd Qu.:23.0  
##  Max.   :9.000   Max.   :31.0  
## 
# tworzymy dodatkowe braki danych
data[4:10,3] <- rep(NA,7)
data[1:5,4] <- NA
summary(data)
##      Ozone           Solar.R           Wind             Temp      
##  Min.   :  1.00   Min.   :  7.0   Min.   : 1.700   Min.   :57.00  
##  1st Qu.: 18.00   1st Qu.:115.8   1st Qu.: 7.400   1st Qu.:73.00  
##  Median : 31.50   Median :205.0   Median : 9.700   Median :79.00  
##  Mean   : 42.13   Mean   :185.9   Mean   : 9.806   Mean   :78.28  
##  3rd Qu.: 63.25   3rd Qu.:258.8   3rd Qu.:11.500   3rd Qu.:85.00  
##  Max.   :168.00   Max.   :334.0   Max.   :20.700   Max.   :97.00  
##  NA's   :37       NA's   :7       NA's   :7        NA's   :5      
##      Month            Day      
##  Min.   :5.000   Min.   : 1.0  
##  1st Qu.:6.000   1st Qu.: 8.0  
##  Median :7.000   Median :16.0  
##  Mean   :6.993   Mean   :15.8  
##  3rd Qu.:8.000   3rd Qu.:23.0  
##  Max.   :9.000   Max.   :31.0  
## 
md.pattern(data)

##     Month Day Temp Solar.R Wind Ozone   
## 104     1   1    1       1    1     1  0
## 34      1   1    1       1    1     0  1
## 3       1   1    1       1    0     1  1
## 1       1   1    1       1    0     0  2
## 4       1   1    1       0    1     1  1
## 1       1   1    1       0    1     0  2
## 1       1   1    1       0    0     1  2
## 3       1   1    0       1    1     1  1
## 1       1   1    0       1    0     1  2
## 1       1   1    0       0    0     0  4
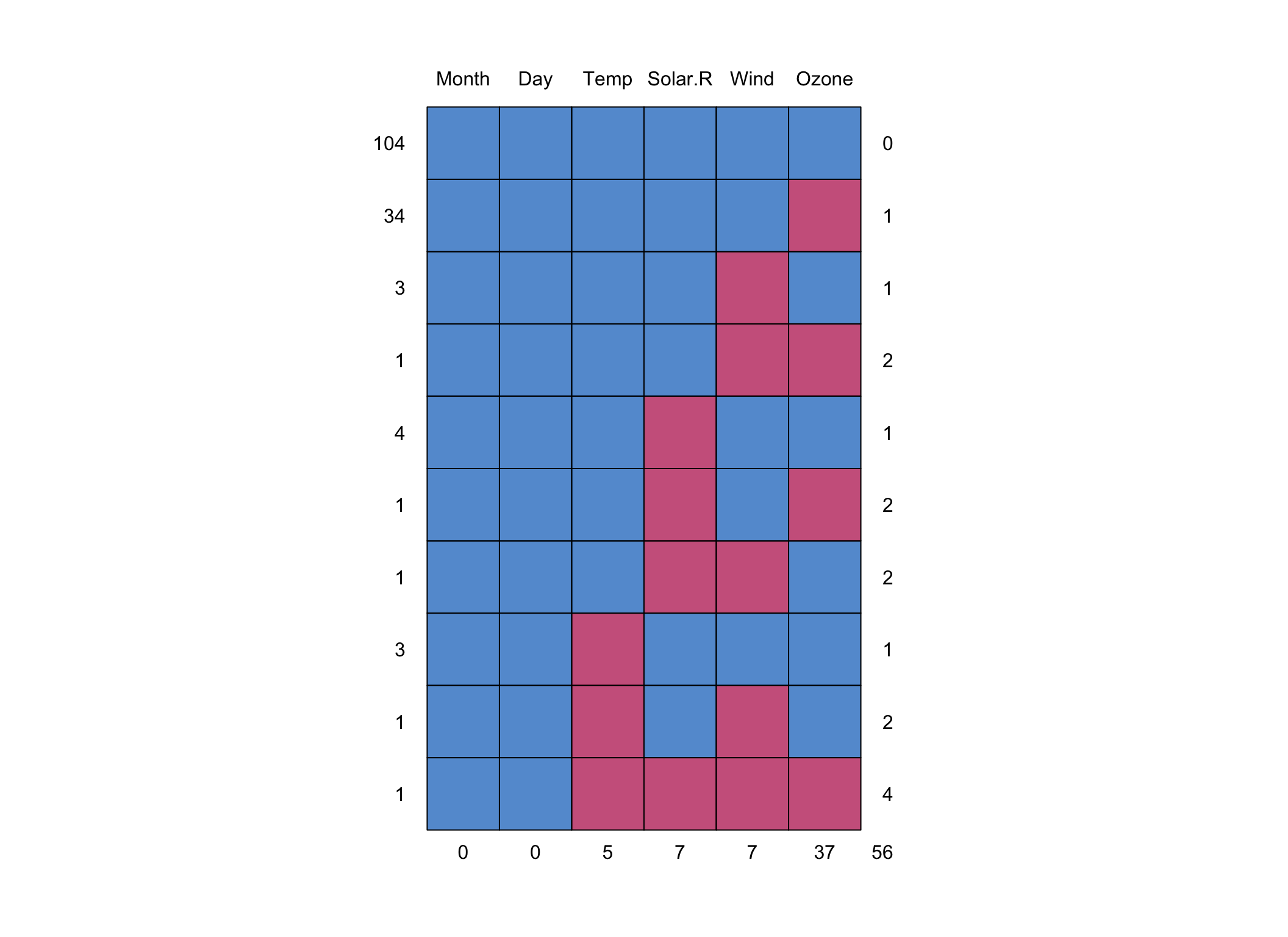
##         0   0    5       7    7    37 56

Do ilustracji braków danych można zastosować funkcje pakietu VIM.

library(VIM)
aggr(data, numbers=TRUE, 
     sortVars=TRUE, 
     labels=names(data), 
     cex.axis=.7)

## 
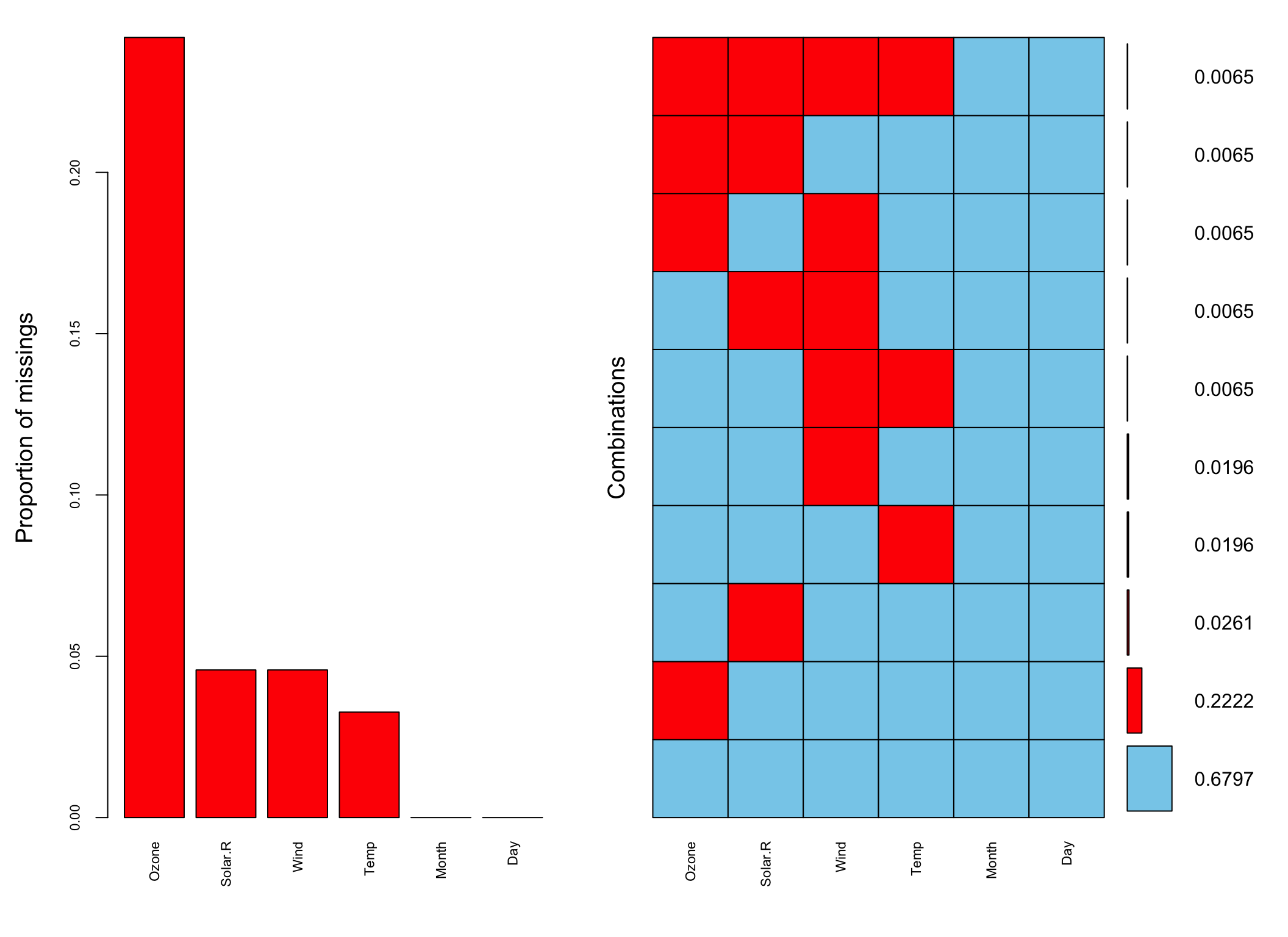
##  Variables sorted by number of missings: 
##  Variable      Count
##     Ozone 0.24183007
##   Solar.R 0.04575163
##      Wind 0.04575163
##      Temp 0.03267974
##     Month 0.00000000
##       Day 0.00000000

Tak przedstawia się wykres rozrzutu zmiennych Ozone i Solar.R z uwzględnieniem położenia braków danych.

marginplot(data[c(1,2)])

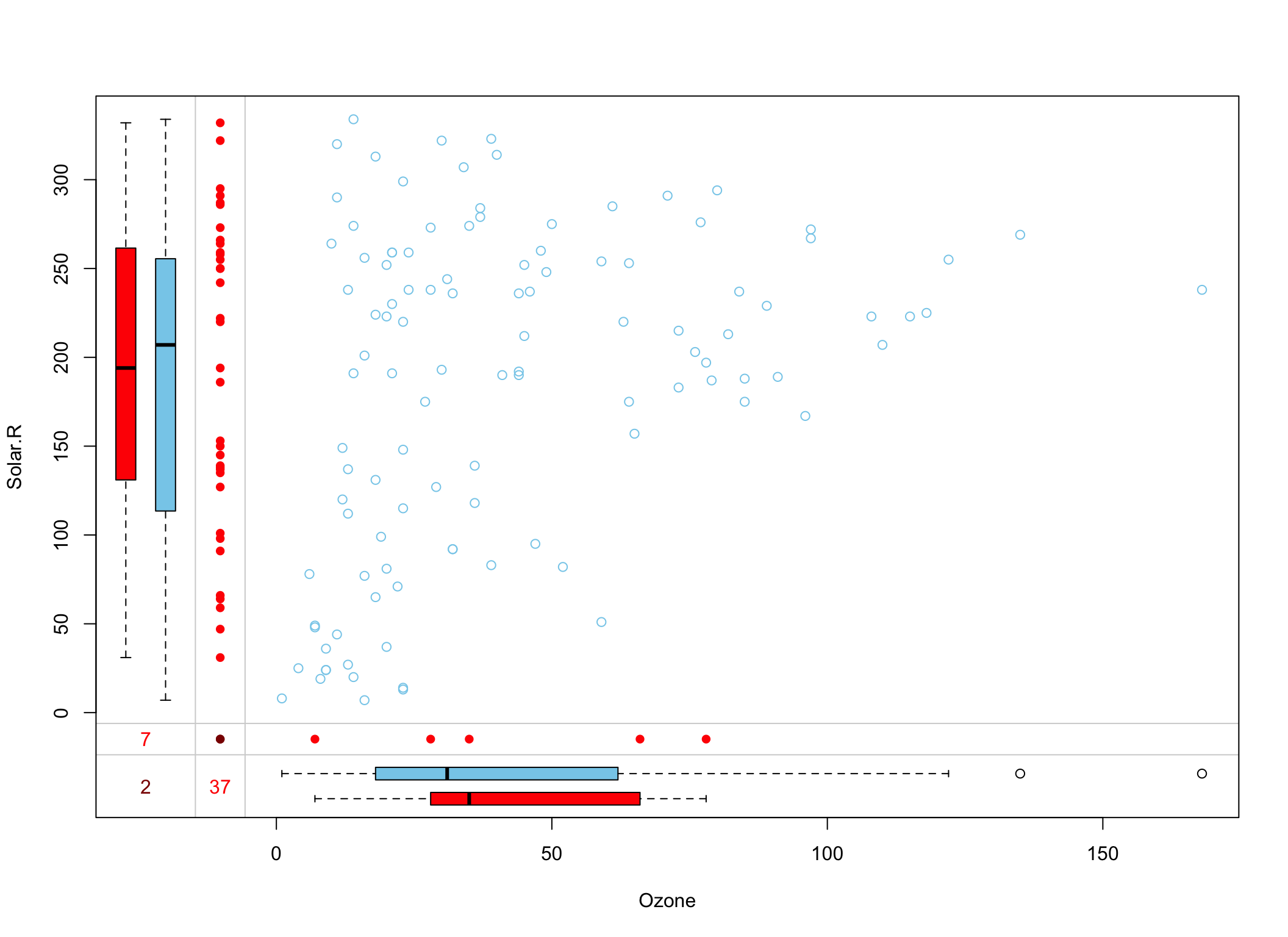
Dokonamy imputacji metodą pmm.

tempData <- mice(data, 
                 maxit=50, 
                 meth='pmm', 
                 seed=44, 
                 printFlag = F)
summary(tempData)
## Class: mids
## Number of multiple imputations:  5 
## Imputation methods:
##   Ozone Solar.R    Wind    Temp   Month     Day 
##   "pmm"   "pmm"   "pmm"   "pmm"      ""      "" 
## PredictorMatrix:
##         Ozone Solar.R Wind Temp Month Day
## Ozone       0       1    1    1     1   1
## Solar.R     1       0    1    1     1   1
## Wind        1       1    0    1     1   1
## Temp        1       1    1    0     1   1
## Month       1       1    1    1     0   1
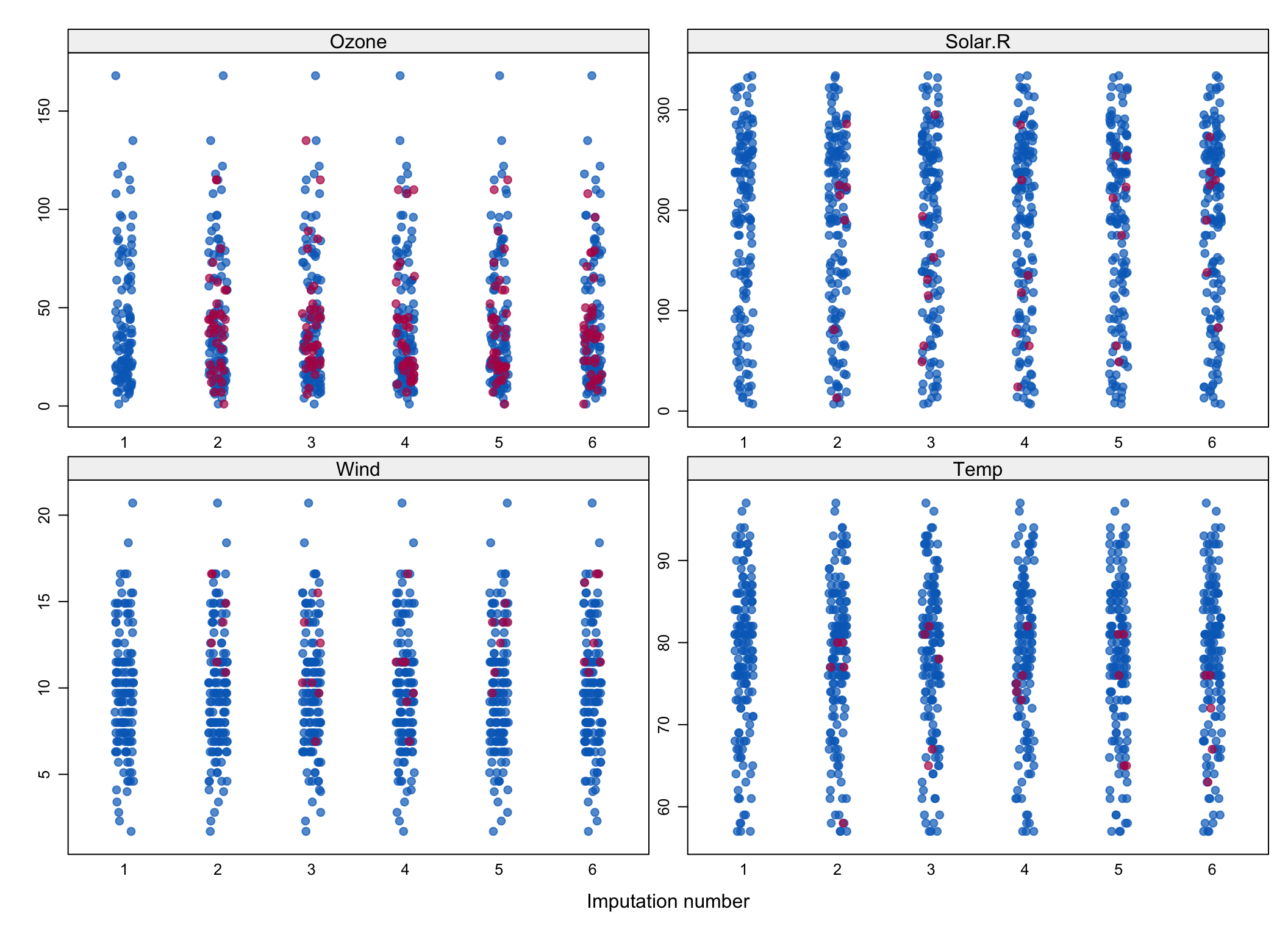
## Day         1       1    1    1     1   0

Ponieważ, funkcja mice domyślnie dokonuje 5 kompletnych imputacji, możemy się przekonać jak bardzo różnią się poszczególne imputacje i zdecydować się na jedną z nich.

head(tempData$imp$Ozone)
##     1  2  3  4  5
## 5  12  9 28 24 11
## 10  1 34 18 21 23
## 25 18  6 37 18  8
## 26 37 19 13 19 37
## 27 32 23 20 21 23
## 32 47 41 16 59 28

Ostatecznie imputacji dokonujemy wybierając jeden z zestawów danych uzupełniających (np. pierwszy).

completedData <- mice::complete(tempData, 1)
summary(completedData)
##      Ozone           Solar.R           Wind             Temp      
##  Min.   :  1.00   Min.   :  7.0   Min.   : 1.700   Min.   :57.00  
##  1st Qu.: 18.00   1st Qu.:115.0   1st Qu.: 7.400   1st Qu.:73.00  
##  Median : 35.00   Median :207.0   Median : 9.700   Median :79.00  
##  Mean   : 41.72   Mean   :185.5   Mean   : 9.991   Mean   :78.15  
##  3rd Qu.: 59.00   3rd Qu.:258.0   3rd Qu.:12.000   3rd Qu.:85.00  
##  Max.   :168.00   Max.   :334.0   Max.   :20.700   Max.   :97.00  
##      Month            Day      
##  Min.   :5.000   Min.   : 1.0  
##  1st Qu.:6.000   1st Qu.: 8.0  
##  Median :7.000   Median :16.0  
##  Mean   :6.993   Mean   :15.8  
##  3rd Qu.:8.000   3rd Qu.:23.0  
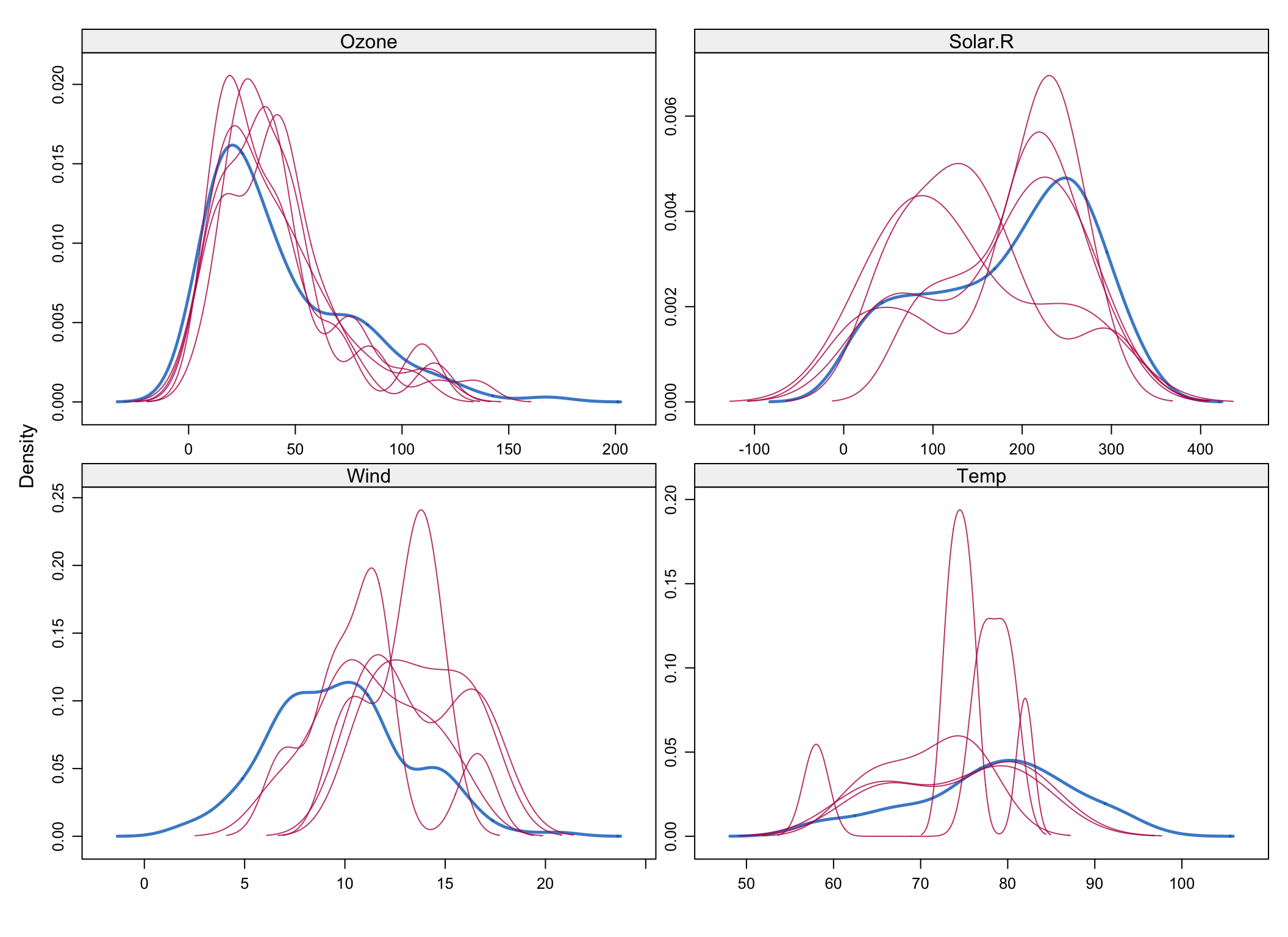
##  Max.   :9.000   Max.   :31.0

Za pomocą funkcji pakietu mice możemy również przedstawić graficznie gdzie i jak zostały uzupełnione dane.

densityplot(tempData, ~Ozone+Solar.R+Wind+Temp)

stripplot(tempData, Ozone+Solar.R+Wind+Temp~.imp, pch = 20, cex = 1.2)

Bibliografia

Firke, Sam. 2018. Janitor: Simple Tools for Examining and Cleaning Dirty Data. https://CRAN.R-project.org/package=janitor.
Templ, Matthias, Alexander Kowarik, Andreas Alfons, and Bernd Prantner. 2019. VIM: Visualization and Imputation of Missing Values. https://CRAN.R-project.org/package=VIM.
Torgo, Luis. 2013. DMwR: Functions and Data for "Data Mining with r". https://CRAN.R-project.org/package=DMwR.
van Buuren, Stef, and Karin Groothuis-Oudshoorn. 2018. Mice: Multivariate Imputation by Chained Equations. https://CRAN.R-project.org/package=mice.

  1. polega na usuwaniu wierszy zawierających braki↩︎

  2. więcej o zjawisku przeuczenia w dalszej części książki↩︎