12 Metoda wektorów nośnych
12.1 Wprowadzenie
Metoda wektorów nośnych21 (ang. Support Vector Machines) to kolejna metoda klasyfikacji obserwacji na podstawie cech (atrybutów). Jest techniką z nauczycielem tzn., że w próbie uczącej występują zarówno cechy charakteryzujące badane obiekty jak i ich przynależność do klasy.
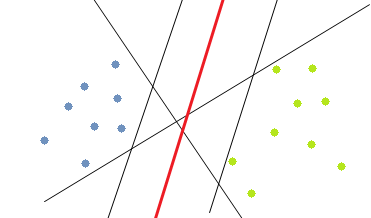
Rysunek 12.1: Przykład prostych separujących obiekty obu grup
12.2 Definicja modelu dla klas liniowo separowalnych
Istotą tej metody jest znalezienie wektorów nośnych, definiujących hiperpowierzchnie optymalnie separujące obiekty w homogeniczne grupy.
Niech \(D\) będzie zbiorem \(n\) punktów w \(d\)-wymiarowej przestrzeni określonych następująco \((\vec{x}_i, y_i)\), \(i=1,\ldots, d\), gdzie \(y_i\) przyjmuje wartości -1 lub 1 w zależności od tego do której grupy należy (zakładamy istnienie tylko dwóch grup). Poszukujemy takiej hiperpłaszczyzny, która maksymalizuje margines pomiędzy punktami obu klas w przestrzeni cech \(\vec{x}\).
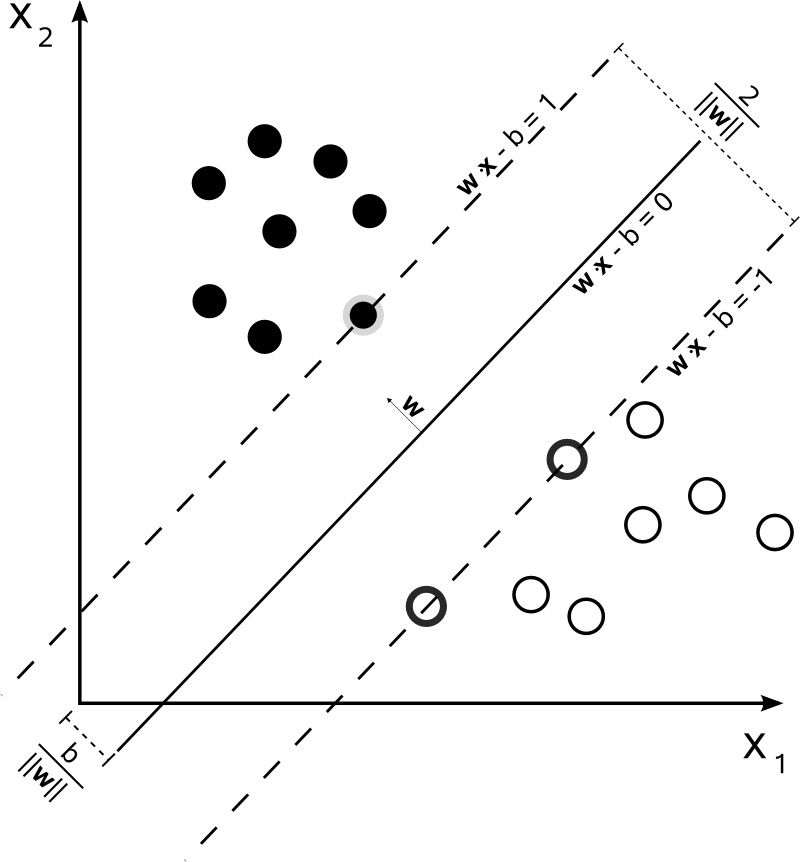
Rysunek 12.2: Płaszczyzna najlepiej rozdzielająca obiekty obu grup (białe i czarne kropki) wraz z prostymi wyznaczającymi maksymalny margines separujący obie grupy
Margines ten jest określany jako najmniejsza odległość pomiędzy hiperpłaszczyzną i elementami z każdej z grup. Dowolna hiperpłaszczyzna może być zapisana równaniem \(\vec{w}\vec{x}-b=0\), gdzie \(\vec{w}\) jest wektorem normalnym do hiperpłaszczyzny. Jeśli dane są liniowo separowalne to, można wybrać takie dwie hiperpłaszczyzny, że odległość pomiędzy nimi jest największa. Równania tych hiperpłaszczyzn dane są wzorami \[\begin{equation} \vec{w}\vec{x}-b=1, \quad \vec{w}\vec{x}-b=-1 \tag{12.1} \end{equation}\]
Odległość pomiędzy tymi hiperpłaszczyznami wynosi \(\tfrac{2}{\|\vec{w}\|}\). Zatem żeby zmaksymalizować odległość pomiędzy hiperpłaszczyznami (margines) musimy zminimalizować \(\tfrac{\|\vec{w}\|}{2}\). Dodatkowo, żeby nie pozwolić aby punkty wpadały do marginesu musimy nałożyć dodatkowe ograniczenia \[\begin{align} \vec{w}\vec{x}_i-b\geq& 1, \quad y_i=1\\ \vec{w}\vec{x}_i-b\leq& -1, \quad y_i=-1 \tag{12.2} \end{align}\] Co można zapisać prościej \[\begin{equation} y_i(\vec{w}\vec{x}_i-b)\geq 1,\quad 1\leq i\leq n. \tag{12.3} \end{equation}\] Zatem \(\vec{w}\) i \(b\) minimalizujące \(\|\vec{w}\|\) przy jednoczesnym spełnieniu warunku \(\eqref{hiper3}\) definiują klasyfikator postaci \[\begin{equation} \vec{x}\rightarrow \operatorname{sgn}(\vec{w}\vec{x}-b). \tag{12.4} \end{equation}\]
Z racji, że \(\|\vec{w}\|\) jest określona jako pierwiastek sumy kwadratów poszczególnych współrzędnych wektora, to częściej w minimalizacji stosuje się \(\|\vec{w}\|^2\).
Sformułowany powyżej problem należy do grupy optymalizacji funkcji kwadratowej przy liniowych ograniczeniach. Rozwiązuje się go metodą mnożników Lagrange’a.
Minimalizujemy funkcję \[\begin{equation} L(w, b, \alpha) = \frac{1}{2}\|\vec{w}\|^2-\sum_{i=1}^{n}\alpha_i\big(y_i(\vec{w}\vec{x}_i-b)-1\big), \tag{12.5} \end{equation}\] gdzie \(\alpha_i\) są mnożnikami Lagrange’a.
Niestety rozwiązanie takiego równania różniczkując po \(\vec{w}\) i \(b\) i przyrównując do zera nie jest łatwe. Dlatego Karush-Kuhn Tucker wprowadzili ograniczenia na mnożniki \(\alpha_i\geq 0\) oraz \(\alpha_i\big(y_i(\vec{w}\vec{x}_i-b)-1\big)=0\). Co w konsekwencji powoduje, że \(\alpha_i\) są niezerowe jedynie dla wektorów nośnych, a dla pozostałych 0.
Dalej jednak poszukiwanie rozwiązania zagadnienia minimalizacji funkcji \(L\) ze względu na tak wiele parametrów może być uciążliwe. Wówczas stosuje się maksymalizację dualnej wersji22 \[\begin{equation} L_D(\alpha) = \sum_{i=1}^{n}\alpha_i+\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jy_iy_j\vec{x}_i'\vec{x}_j \tag{12.6} \end{equation}\] przy ograniczeniach \(\alpha_i\geq 0\) i \(\sum_{i=1}^{n}\alpha_iy_i=0\).
Rozwiązaniem powyższego zagadnienia jest \[\begin{align} \vec{w}=&\sum_{i=1}^{n}\alpha_iy_i\vec{x}_i,\tag{12.7}\\ b=&y_i-\vec{w}\vec{x}_i, \tag{12.8} \end{align}\] a hiperpłaszczyzna decyzyjna \[\begin{equation} \sum_{i=1}^{n}\alpha_iy_i\vec{x}_i\vec{x}-b=0, \tag{12.9} \end{equation}\] gdzie \(\vec{x}_i\) są wektorami nośnymi ze zbioru uczącego, a \(\vec{x}\) jest nowym wektorem dla którego przeprowadzamy klasyfikację. Należy również zauważyć, że im większa wartość \(\alpha_i\), tym większy wpływ wektora na granicę decyzyjną.
12.3 Definicja modelu dla klas nieliniowo separowalnych
Niestety rzadko przestrzeń atrybutów jest liniowo separowalna. Stosuje się wówczas modyfikację powyższej metody przez wprowadzenie następującej funkcji straty \[\begin{equation} \zeta_i=\max\big(0,1-y_i(\vec{w}\vec{x}_i-b)\big). \tag{12.10} \end{equation}\] Zauważmy, że \(\zeta_i\) jest najmniejszą liczbą nieujemną spełniającą nierówność \[\begin{equation} y_i(\vec{w}\vec{x}_i-b)\geq 1-\zeta_i. \tag{12.11} \end{equation}\] Możemy ją interpretować tak, że jeśli warunek (12.3) jest spełniony, czyli punkty leżą na zewnątrz marginesu (po właściwych stronach), to funkcja straty przyjmuje wartość 0. W przeciwnym przypadku wartość funkcji jest proporcjonalna do odległości od brzegu marginesu. Dlatego wystarczy zminimalizować wartość \[\begin{equation} \frac{1}{n}\sum_{i=1}^{n}\zeta_i+\lambda\|\vec{w}\|^2, \tag{12.12} \end{equation}\] przy warunku (12.11) i \(\zeta_i\geq 0\) oraz gdzie \(\lambda\) jest wagą kompromisu pomiędzy szerokością marginesu a zapewnieniem, że punkty leżą po właściwych stronach marginesu. Przy dostatecznie małych wartościach \(\lambda\) i separowalności liniowej punktów przestrzeni atrybutów powyższy klasyfikator będzie się zachowywał podobnie jak (12.4).
Rozwiązanie problemu minimalizacji funkcji straty określonej w (12.12) za pomocą dualnej wersji mnożników Lagrange’a sprowadza się do minimalizacji funkcji \[\begin{equation} L(\alpha_i) = \sum_{i=1}^{n}\alpha_i+\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jy_iy_j\vec{x}_i'\vec{x}_j, \tag{12.13} \end{equation}\] przy warunkach \[\begin{equation} \sum_{i=1}^{n}\alpha_iy_i=0,\quad 0\leq \alpha_i\leq \frac{1}{2n\lambda}. \tag{12.14} \end{equation}\] Wektor normalny do hiperpłaszczyzny jest postaci \[\begin{equation} \vec{w}=\sum_{i=1}^{n}\alpha_iy_i\vec{x}_i, \tag{12.15} \end{equation}\] a parametr \(b\) taki jak w (12.8).
Powyższy algorytm został przedstawiony przez Vapnika w 1963 roku jako klasyfikator liniowy ale dopiero po wprowadzeniu funkcji jądrowych przekształcających liniowy brzeg decyzyjny na nieliniowy, metoda ta zyskała w oczach statystyków.
12.4 Definicja modelu jądrowego
W roku 1992 Boser, Guyon i Vapnik wprowadzili pojęcie nieliniowego klasyfikatora opartego na metodzie wektorów nośnych, który było uogólnieniem techniki przedstawionej przez Vapnika w 1963 roku. Pozwala ona na nieliniowy kształt brzegu obszaru decyzyjnego.
Zasada działania polega na znalezieniu takiego jądra przekształcenia (ang. kernel) \(\phi\), które odwzoruje przestrzeń \(d\)-wymiarową w \(d'\)-wymiarową, gdzie \(d'>d\) taką, że \(D_{\phi}=\{\phi(\vec{x}_i), y_i\}\) jest możliwie jak najbardziej separowalna.
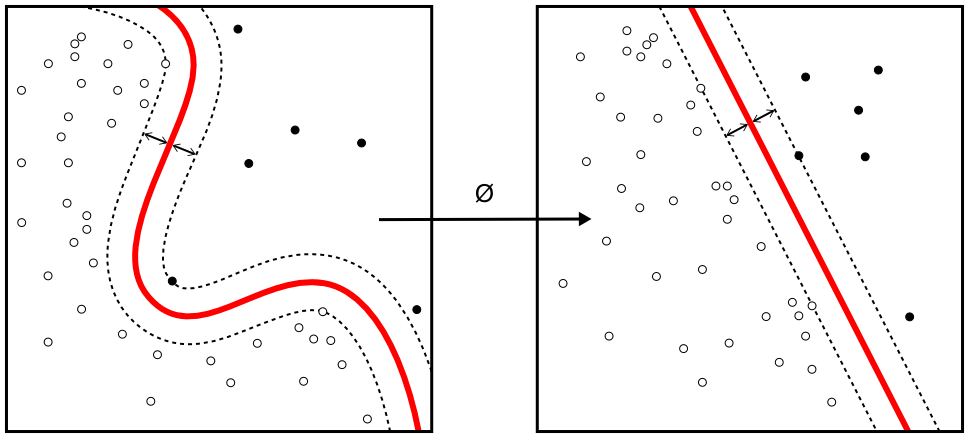
Rysunek 12.3: Przykład zastosowania takiego przekształcenia jądrowego aby z sytuacji braku liniowej separowalności do niej doprowadzić
Dla funkcji jądrowej określonej wzorem \(k(\vec{x}_i,\vec{x}_j)=\phi(\vec{x}_i)\phi(\vec{x}_j)\) przeprowadzamy identyczne rozumowanie jak w przypadku liniowych brzegów obszarów decyzyjnych. Minimalizujemy zatem wyrażenie \[\begin{align} L(\alpha_i) =& \sum_{i=1}^{n}\alpha_i+\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jy_iy_j\phi(\vec{x}_i)\phi(\vec{x}_j)\\ =&\sum_{i=1}^{n}\alpha_i+\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jy_iy_jk(\vec{x}_i,\vec{x}_j), \tag{12.16} \end{align}\] przy warunkach \[\begin{equation} \sum_{i=1}^{n}\alpha_iy_i=0,\quad 0\leq \alpha_i\leq \frac{1}{2n\lambda}. \tag{12.17} \end{equation}\] Rozwiązanie powyższego problemu są również podobne do ich liniowych odpowiedników \[\begin{equation} \vec{w}=\sum_{i=1}^{n}\alpha_iy_i\phi(\vec{x}_i), \tag{12.18} \end{equation}\] a parametr \(b=\vec{w}\phi(\vec{x}_i)-y_i\).
Najczęściej stosowanymi funkcjami jądrowymi są:
- wielomianowa \(k(\vec{x}_i,\vec{x}_j)=(a\vec{x}_i'\vec{x}_j+b)^q\),
- gaussowska \(k(\vec{x}_i,\vec{x}_j)=\exp(-\gamma\|\vec{x}_i-\vec{x}_j\|^2)\),
- Laplace’a \(k(\vec{x}_i,\vec{x}_j)=\exp(-\gamma\|\vec{x}_i-\vec{x}_j\|)\),
- hiperboliczna \(k(\vec{x}_i,\vec{x}_j)=\tanh(\vec{x}_i'\vec{x}_j+b)\),
- sigmoidalna \(k(\vec{x}_i,\vec{x}_j)=\tanh(a\vec{x}_i'\vec{x}_j+b)\),
- Bessel’a \(k(\vec{x}_i,\vec{x}_j)=\frac{Bessel^n_{(\nu+1)}(\sigma\|\vec{x}_i-\vec{x}_j\|)}{(\|\vec{x}_i-\vec{x}_j\|)^{n(\nu+1)}}\),
- ANOVA \(k(\vec{x}_i,\vec{x}_j)=\left(\sum_{k=1}^{n}\exp\big(-\sigma(x^k_i-x^k_j)^2\big)\right)^d\),
- sklejana dla jednowymiarowej przestrzeni \(k(x_i,x_j)=1+x_ix_j\min(x_i,x_j)-\frac{x_i+x_j}{2}\big(\min(x_i,x_j)\big)^2+\frac{(\min(x_i,x_j))^3}{3}\).
W przypadku braku wiedzy o danych funkcja gaussowska, Laplace’a i Bessel’a są zalecane.
Przykłady obszarów zastosowań:
- w kategoryzacji tekstu i hipertekstu;
- klasyfikacji obrazów - rezultaty eksperymentów pokazują, że SVM daje lepsze rezultaty niż inne techniki;
- rozpoznawanie obiektów 3D;
- odnajdowanie włamań do systemu;
- rozpoznawanie pisma ręcznego;
- odkrywanie ukrytych treści na zdjęciach;
- klasyfikacja protein;
- odnajdowanie sekwencji kodu genetycznego
- itp…
12.5 Zalety i wady
Mocne strony:
- stopień skomplikowania nie jest zależny od wymiaru przestrzeni atrybutów;
- optymalny klasyfikator (znajduje minimum globalne);
- nie jest czuły na przetrenowanie;
- bardzo duża skuteczność w praktyce.
Słabe strony:
- przy dużej ilości danych estymacja modelu może trwać długo;
- estymacja poprawnego modelu wymaga pewnej wiedzy;
- nie ma miejsca na wprowadzenie własnej wiedzy.