4 Drzewa decyzyjne

Drzewo decyzyjne11 jest strukturą hierarchiczną przedstawiającą model klasyfikacyjny lub regresyjny. Stosowane są szczególnie często wówczas, gdy funkcyjna postać związku pomiędzy predyktorami a zmienną wynikową jest nieznana lub ciężka do ustalenia. Każde drzewo decyzyjne składa się z korzenia (ang. root), węzłów (ang. nodes) i liści (ang. leaves). Korzeniem nazywamy początkowy węzeł drzewa, z którego poprzez podziały (ang. splits) powstają kolejne węzły potomne. Końcowe węzły, które nie podlegają podziałom nazywamy liśćmi, a linie łączące węzły nazywamy gałęziami (ang. branches).

Jeśli drzewo służy do zadań klasyfikacyjnych, to liście zawierają informację o tym, która klasa w danym ciągu podziałów jest najbardziej prawdopodobna. Natomiast, jeśli drzewo jest regresyjne, to liście zawierają warunkowe miary tendencji centralnej (najczęściej średnią) wartości zmiennej wynikowej. Warunek stanowi szereg podziałów doprowadzający do danego węzła terminalnego (liścia). W obu przypadkach (klasyfikacji i regresji) drzewo “dąży” do takiego podziału by kolejne węzły, a co za tym idzie również liście, były ja najbardziej jednorodne ze względu na zmienną wynikową.

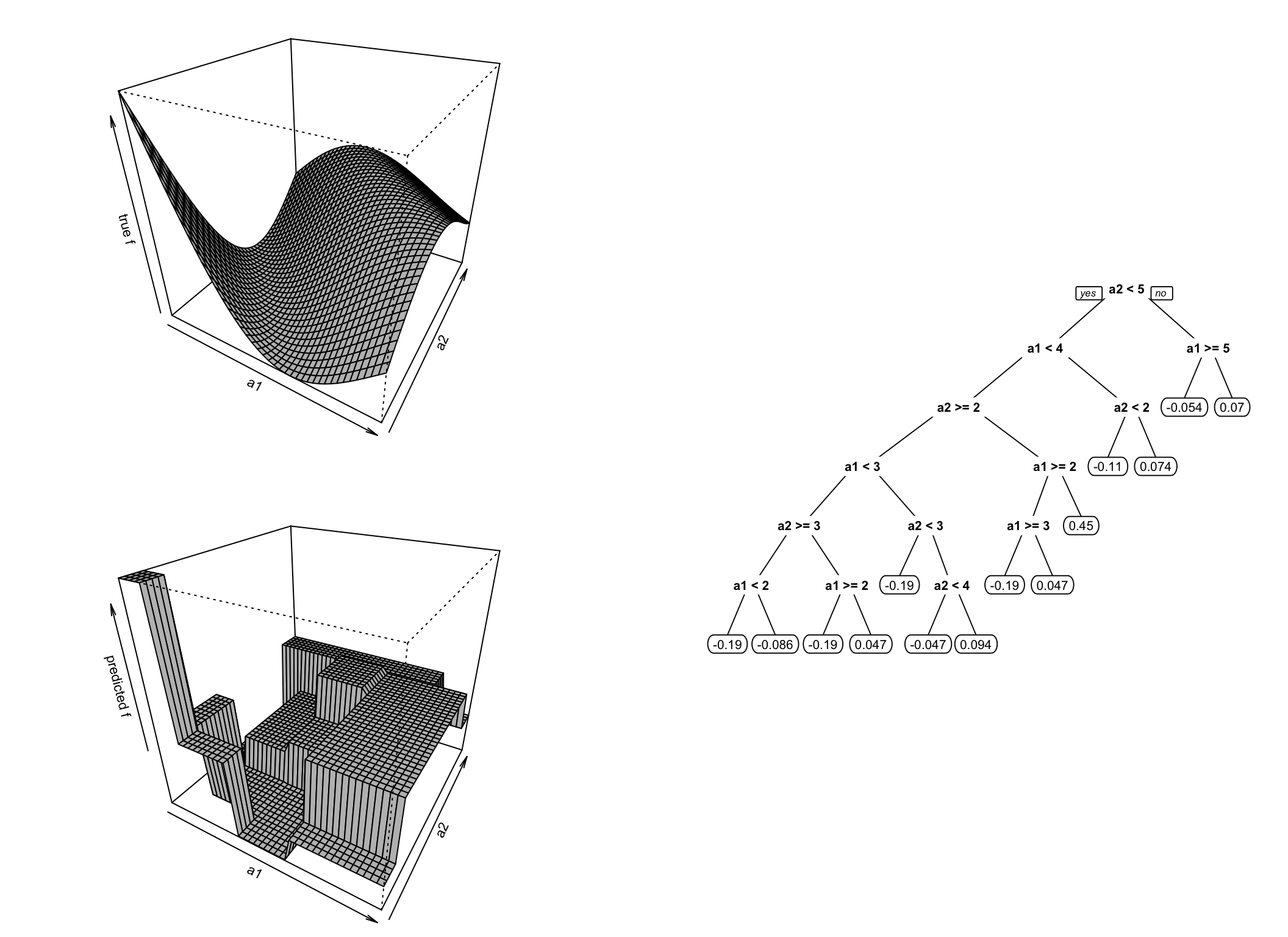
Przykład działania drzewa regresyjnego. Wykes w lewym górnym rogu pokazuje prawdziwą zależność, wyres po prawej stronie jest ilustracją drzewa decyzyjnego, a wykres w lewym dolnym rogu pokazuje dyskretyzację przestrzeni dokonaną przez drzewo, czyli sposób jego działania.

Rysunek 4.1: Przykład działania drzewa regresyjnego. Wykes w lewym górnym rogu pokazuje prawdziwą zależność, wyres po prawej stronie jest ilustracją drzewa decyzyjnego, a wykres w lewym dolnym rogu pokazuje dyskretyzację przestrzeni dokonaną przez drzewo, czyli sposób jego działania.

4.1 Węzły i gałęzie

Każdy podział rozdziela dziedzinę \(X\) na dwa lub więcej podobszarów dziedziny i wówczas każda obserwacja węzła nadrzędnego jest przyporządkowana węzłom potomnym. Każdy odchodzący węzeł potomny jest połączony gałęzią, która to wiąże się ściśle z możliwymi wynikami podziału. Każdy \(\mathbf{n}\)-ty węzeł można opisać jako podzbiór dziedziny w następujący sposób \[\begin{equation} X_{\mathbf{n}}=\{x\in X|t_1(x)=r_1,t_2(x)=r_2,\ldots,t_k(x)=r_k\}, \end{equation}\] gdzie \(t_1,t_2,\ldots,t_k\) są podziałami, które przeprowadzają \(x\) w obszary \(r_1, r_2,\ldots, r_k\). Przez \[\begin{equation} S_{\mathbf{n}, t=r}=\{x\in S|t(x)=r\} \end{equation}\] rozumiemy, że dokonano takiego ciągu podziałów zbioru \(S\), że jego wartości znalazły się w \(\mathbf{n}\)-tym węźle.

4.2 Rodzaje reguł podziału

Najczęściej występujące reguły podziału w drzewach decyzyjnych są jednowymiarowe, czyli warunek podziału jest generowany na podstawie jednego atrybutu. Istnieją podziały wielowymiarowe ale ze względu na złożoność obliczeniową są rzadziej stosowane.

4.2.1 Podziały dla atrybutów ze skali nominalnej

Istnieją dwa typy reguł podziału dla skali nominalnej:

  • oparte na wartości atrybutu (ang. value based) - wówczas funkcja testowa przyjmuje postać \(t(x)=a(x)\), czyli podział generują wartości atrybutu;
  • oparte na równości (ang. equality based) - gdzie funkcja testowa jest zdefiniowana jako \[\begin{equation} t(x)= \begin{cases} 1, &\text{ gdy } a(x)=\nu\\ 0, & \text{ w przeciwnym przypadku}, \end{cases} \end{equation}\] gdzie \(\nu\in A\) i \(A\) jest zbiorem możliwych wartości \(a\). W tym przypadku podział jest dychotomiczny, albo obiekt ma wartość atrybutu równą \(\nu\), albo go nie ma.

4.2.2 Podziały dla atrybutów ze skali ciągłej

Reguły podziału stosowane do skali ciągłej, to:

  • oparta na nierównościach (ang. inequality based) - zdefiniowana jako \[\begin{equation} t(x) = \begin{cases} 1, &\text{ gdy }a(x)\leq \nu\\ 0, & \text{w przeciwnym przypadku}, \end{cases} \end{equation}\] gdzie \(\nu\in A\);
  • przedziałowa (ang. interval based) - zdefiniowana jako \[\begin{equation} t(x) = \begin{cases} 1, &\text{ gdy }a(x) \in I_1\\ 2, &\text{ gdy }a(x) \in I_2\\ \vdots & \\ k, &\text{ gdy }a(x) \in I_k\\ \end{cases} \end{equation}\] gdzie \(I_1,I_2,\ldots,I_k\subset A\) stanowią rozłączny podział (przedziałami) przeciwdziedziny \(A\).

4.2.3 Podziały dla atrybutów ze skali porządkowej

Podziały te mogą wykorzystywać oba wcześniej wspomniane typy, w zależności od potrzeb.

4.3 Algorytm budowy drzewa

  1. stwórz początkowy węzeł (korzeń) i oznacz go jako otwarty;
  2. przypisz wszystkie możliwe rekordy do węzła początkowego;
  3. dopóki istnieją otwarte węzły wykonuj:
    • wybierz węzeł \(\mathbf{n}\), wyznacz potrzebne statystyki opisowe zmiennej zależnej dla tego węzła i przypisz wartość docelową;
    • jeśli kryterium zatrzymania podziału jest spełnione dla węzła \(n\), to oznacz go za zamknięty;
    • w przeciwnym przypadku wybierz podział \(r\) elementów węzła \(\mathbf{n}\), i dla każdego podzbioru podziału stwórz węzeł niższego rzędu (potomka) \(\mathbf{n}_r\) oraz oznacz go jako otwarty;
    • następnie przypisz wszystkie przypadki generowane podziałem \(r\) do odpowiednich węzłów potomków \(\mathbf{n}_r\);
    • oznacza węzeł \(\mathbf{n}\) jako zamknięty.

Sposób przypisywania wartości docelowej wiąże się ściśle z rodzajem drzewa. W drzewach regresyjnych chodzi o wyliczenie średniej lub mediany dla obserwacji ujętych w danym węźle. Natomiast w przypadku drzewa klasyfikacyjnego, wyznacza się wartości prawdopodobieństw przynależności obserwacji znajdującej się w danym węźle do poszczególnych klas \[\begin{equation} \P(d|\mathbf{n})=\P_{T_\mathbf{n}}(d)=\frac{|T_\mathbf{n}^d|}{|T_\mathbf{n}|}, \end{equation}\] gdzie \(T_\mathbf{n}\) oznaczają obserwacje zbioru uczącego znajdujące się w węźle \(\mathbf{n}\), a \(T_\mathbf{n}^d\) oznacza dodatkowo podzbiór zbioru uczącego w \(\mathbf{n}\) węźle, które należą do klasy \(d\). Oczywiście klasyfikacja na podstawie otrzymanych prawdopodobieństw w danym węźle jest dokonana przez wybór klasy charakteryzującej się najwyższym prawdopodobieństwem.

4.4 Kryteria zatrzymania

Kryterium zatrzymania jest warunkiem, który decyduje o tym, że dany węzeł uznajemy za zamknięty i nie dokonujemy dalszego jego podziału. Wyróżniamy następujące kryteria zatrzymania:

  • jednorodność węzła - w przypadku drzewa klasyfikacyjnego może zdarzyć się sytuacja, że wszystkie obserwacje węzła będą pochodziły z jednej klasy. Wówczas nie ma sensu dokonywać dalszego podziału węzła;
  • węzeł jest pusty - zbiór przypisanych obserwacji zbioru uczącego do \(\mathbf{n}\)-tego węzła jest pusty;
  • brak reguł podziału - wszystkie reguły podziału zostały wykorzystane, zatem nie da się stworzyć potomnych węzłów, które charakteryzowałyby się większą homogenicznością;

Warunki ujęte w pierwszych dwóch kryteriach mogą być nieco złagodzone, poprzez zatrzymanie podziałów wówczas, gdy prawdopodobieństwo przynależenia do pewnej klasy przekroczy ustalony próg lub gdy liczebność węzła spadnie poniżej ustalonej wartości.

W literaturze tematu istnieje jeszcze jedno często stosowane kryterium zatrzymania oparte na wielkości drzewa. Węzeł potomny ustala się jako zamknięty, gdy długość ścieżki dojścia do nie go przekroczy ustaloną wartość.

4.5 Reguły podziału

Ważnym elementem algorytmu tworzenia drzewa regresyjnego jest reguła podziału. Dobierana jest w taki sposób aby zmaksymalizować zdolności generalizacyjne drzewa. Złożoność drzewa mierzona jest najczęściej przeciętną liczbą podziałów potrzebnych do dotarcia do liścia zaczynając od korzenia. Liście są najczęściej tworzone wówczas gdy dyspersja wartości wynikowej jest stosunkowo mała lub węzeł zawiera w miarę homogeniczne obserwacje ze względu na przynależność do klasy zmiennej wynikowej. W przypadku drzew regresyjnych zmienność na poziomie węzłów jest dobrą miarą służącą do definiowania podziału w węźle. I tak, jeśli pewien podział generuje nam stosunkowo małe dyspersje wartości docelowych w węzłach potomnych, to można ten podział uznać za właściwy. Jeśli \(T_n\) oznacza zbiór rekordów należących do węzła \(n\), a \(T_{n,t=r}\) są podzbiorami generowanymi przez podział \(r\) w węzłach potomnych dla \(n\), to dyspersję wartości docelowej \(f\) będziemy oznaczali następująco \[\begin{equation}\label{dyspersja} \operatorname{disp}_{T_{n,t=r}}(f). \end{equation}\]

Regułę podziału możemy określać poprzez minimalizację średniej ważonej dyspersji wartości docelowej następującej postaci \[\begin{equation}\label{reg_podz} \operatorname{disp}_n(f|t)=\sum_{r\in R_t}\frac{|T_{n,t=r}|}{|T_n|}\operatorname{disp}_{T_{n,t=r}}(f), \end{equation}\] gdzie \(|\ |\) oznacza moc zbioru, a \(R_t\) zbiór wszystkich możliwych wartości reguły podziału. Czasami wygodniej będzie maksymalizować przyrost dyspersji (lub spadek) \[\begin{equation}\label{przyrost} \bigtriangleup \operatorname{disp}_n(f|t)=\operatorname{disp}_n(f)-\sum_{r\in R_t}\frac{|T_{n,t=r}|}{|T_n|}\operatorname{disp}_{T_{n,t=r}}(f). \end{equation}\]

Miarą heterogeniczności węzłów ze względu na zmienną wynikową (ang. impurity) w drzewach klasyfikacyjnych, która pozwala na tworzenie kolejnych podziałów węzła, są najczęściej wskaźnik Gini’ego i entropia (Breiman 1998).

Entropią podzbioru uczącego w węźle \(\mathbf{n}\), wyznaczamy wg wzoru \[\begin{equation} E_{T_{\mathbf{n}}}(c|t) = \sum_{x\in R_t} \frac{|T_{\mathbf{n}, t=r}|}{|T_{\mathbf{n}}|}E_{T_{\mathbf{n}, t=r}}(c), \end{equation}\] gdzie \(t\) jest podziałem (kandydatem), \(r\) potencjalnym wynikiem podziału \(t\), \(c\) jest oznaczeniem klasy zmiennej wynikowej, a \[\begin{equation} E_{T_{\mathbf{n}, t=r}}(c) = \sum_{d\in C}-\P_{T_{\mathbf{n}, t=r}}(c=d)\log\P_{T_{\mathbf{n}, t=r}}(c=d), \end{equation}\] przy czym \[\begin{equation} \P_{T_{\mathbf{n}, t=r}}(c=d)= \P_{T_{\mathbf{n}}}(c=d|t=r). \end{equation}\]

Podobnie definiuje się indeks Gini’ego \[\begin{equation} Gi_{T_{\mathbf{n}}}(c|t) = \sum_{x\in R_t} \frac{|T_{\mathbf{n}, t=r}|}{|T_{\mathbf{n}}|}Gi_{T_{\mathbf{n}, t=r}}(c), \end{equation}\] gdzie \[\begin{equation} Gi_{T_{\mathbf{n}, t=r}}(c) = \sum_{d\in C}\P_{T_{\mathbf{n}, t=r}}(c=d)\cdot(1-\P_{T_{\mathbf{n}, t=r}}(c=d))= 1-\sum_{d\in C}\P^2_{T_{\mathbf{n}, t=r}}(c=d). \end{equation}\] Dla tak zdefiniowanych miar “nieczystości” węzłów, podziału dokonujemy w taki sposób, aby zminimalizować współczynnik Gini’ego lub entropię. Im niższe miary nieczystości, tym bardziej obserwacje znajdujące się w węźle są monokulturą12. Nierzadko korzysta się również z współczynnika przyrostu informacji (ang. information gain) \[\begin{equation} \Delta E_{T_{\mathbf{n}}}(c|t)=E_{T_{\mathbf{n}}}(c)-E_{T_{\mathbf{n}}}(c|t). \end{equation}\] Istnieje również jego odpowiednik dla indeksu Gini’ego. W obu przypadkach optymalnego podziału szukamy poprzez maksymalizację przyrostu informacji.

4.6 Przycinanie drzewa decyzyjnego

Uczenie drzewa decyzyjnego wiąże się z ryzykiem przeuczenia modelu (podobnie jak to się ma w przypadku innych modeli predykcyjnych). Wcześniej przytoczone reguły zatrzymania (np. głębokość drzewa czy zatrzymanie przy osiągnięciu jednorodności na zadanym poziomie) pomagają kontrolować poziom generalizacji drzewa ale czasami będzie dodatkowo potrzebne przycięcie drzewa, czyli usunięcie pewnych podziałów, a co za tym idzie, również liści (węzłów).

4.6.1 Przycinanie redukujące błąd

Jedną ze strategii przycinania drzewa jest przycinanie redukujące błąd (ang. reduced error pruning). Polega ono na porównaniu błędów (najczęściej używana jest miara odsetka błędnych klasyfikacji lub MSE) liścia \(\mathbf{l}\) i węzła do którego drzewo przycinamy \(\mathbf{n}\) na całkiem nowym zbiorze uczącym \(R\). Niech \(e_R(\mathbf{l})\) i \(e_R(\mathbf{n})\) oznaczają odpowiednio błędy na zbiorze \(R\) liścia i węzła. Przez błąd węzła rozumiemy błąd pod-drzewa o korzeniu \(\mathbf{n}\). Wówczas jeśli zachodzi warunek \[\begin{equation} e_R(\mathbf{l})\leq e_R(\mathbf{n}), \end{equation}\] to zaleca się zastąpić węzeł \(\mathbf{n}\) liściem \(\mathbf{l}\).

4.6.2 Przycinanie minimalizujące błąd

Przycinanie minimalizujące błąd opiera się na spostrzeżeniu, że błąd drzewa przyciętego charakteryzuje się zbyt pesymistyczną oceną i dlatego wymaga korekty. Węzeł drzewa klasyfikacyjnego \(\mathbf{n}\) zastępujemy liściem \(\mathbf{l}\), jeśli \[\begin{equation} \hat{e}_T(\mathbf{l})\leq \hat{e}_T(\mathbf{n}), \end{equation}\] gdzie \[\begin{equation} \hat{e}_T(\mathbf{n})=\sum_{\mathbf{n}'\in N(\mathbf{n})}\frac{|T_{\mathbf{n}'}|}{|T_\mathbf{n}|}\hat{e}_T(\mathbf{n}'), \end{equation}\] a \(N(\mathbf{n})\) jest zbiorem wszystkich możliwych węzłów potomnych węzła \(\mathbf{n}\) i \[\begin{equation} \hat{e}_T(\mathbf{l})=1-\frac{|\{x\in T_\mathbf{l}|c(x)=d_{\mathbf{l}}\}|+mp}{|T_\mathbf{l}|+m}, \end{equation}\] gdzie \(p\) jest prawdopodobieństwem przynależności do klasy \(d_{\mathbf{l}}\) ustalona na podstawie zewnętrznej wiedzy (gdy jej nie posiadamy przyjmujemy \(p=1/|C|\)).

W przypadku drzewa regresyjnego znajdujemy wiele analogii, ponieważ jeśli dla pewnego zbioru rekordów \(T\) spełniony jest warunek \[\begin{equation}\label{kryterium1} \operatorname{mse}_T(\mathbf{l})\leq\operatorname{mse}_T(\mathbf{n}), \end{equation}\] gdzie \(\mathbf{l}\) i \(\mathbf{n}\) oznaczają odpowiednio liść i węzeł, to wówczas zastępujemy węzeł \(\mathbf{n}\) przez liść \(\mathbf{l}\).

Estymatory wyznaczone na podstawie niewielkiej próby, mogą być obarczone znaczącym błędem. Wyliczanie błędu średnio-kwadratowego dla podzbioru nowych wartości może się charakteryzować takim obciążeniem. Dlatego stosuje się statystyki opisowe z poprawką, której pochodzenie może mieć trzy źródła: wiedza merytoryczna na temat szukanej wartości, założeń modelu lub na podstawie wyliczeń opartych o cały zbiór wartości.

Skorygowany estymator błędu średnio-kwadratowego ma następującą postać \[\begin{equation}\label{mse} \widehat{\operatorname{mse}}_T(\mathbf{l})=\frac{\sum_{x\in T}(f(x)-m_{\mathbf{l},m,m_0}(f))^2+mS_0^2}{|T_\mathbf{l}|+m}, \end{equation}\] gdzie \[\begin{equation}\label{poprawka} m_{\mathbf{l},m,m_0}(f)=\frac{\sum_{x\in T_\mathbf{l}}f(x)+mm_0}{|T_\mathbf{l}|+m}, \end{equation}\] a \(m_0\) i \(S_0^2\) są średnią i wariancją wyznaczonymi na całej próbie uczącej. Błąd średnio-kwadratowy węzła \(\mathbf{n}\) ma postać \[\begin{equation}\label{propagacja} \widehat{\operatorname{mse}}_T(\mathbf{n})=\sum_{\mathbf{n}'\in N(\mathbf{n})}\frac{|T_{\mathbf{n}'}|}{|T_\mathbf{n}|}\widehat{\operatorname{mse}}_T(\mathbf{n}'). \end{equation}\] Wówczas kryterium podcięcia można zapisać w następujący sposób \[\begin{equation}\label{kryterium2} \widehat{\operatorname{mse}}_T(\mathbf{l}) \leq \widehat{\operatorname{mse}}_T(\mathbf{n}) \end{equation}\]

4.6.3 Przycinanie ze względu na współczynnik złożoności drzewa

Przycinanie ze względu na współczynnik złożoności drzewa (ang. cost-complexity pruning) polega na wprowadzeniu “kary” za zwiększoną złożoność drzewa. Drzewa klasyfikacyjne przycinamy gdy spełniony jest warunek \[\begin{equation} e_T(\mathbf{l})\leq e_T(\mathbf{n})+\alpha C(\mathbf{n}), \end{equation}\] gdzie \(C(\mathbf{n})\) oznacza złożoność drzewa mierzoną liczbą liści, a \(\alpha\) parametrem wagi kary za złożoność drzewa.

Wspomniane kryterium przycięcia dla drzew regresyjnych bazuje na względnym błędzie średnio-kwadratowym (ang. relative square error), czyli \[\begin{equation}\label{rse} \widehat{\operatorname{rse}}_T(\mathbf{n})=\frac{|T|\widehat{\operatorname{mse}}_T(\mathbf{n})}{(|T|-1)S^2_T(f)}, \end{equation}\] gdzie \(T\) oznacza podzbiór \(X\), \(S^2_T\) wariancję na zbiorze \(T\). Wówczas kryterium podcięcia wygląda następująco \[\begin{equation}\label{kryterium3} \widehat{\operatorname{rse}}_T(\mathbf{l})\leq \widehat{\operatorname{rse}}_T(\mathbf{n})+\alpha C(\mathbf{n}). \end{equation}\]

4.7 Obsługa braków danych

Drzewa decyzyjne wyjątkowo dobrze radzą sobie z obsługa zbiorów z brakami. Stosowane są głównie dwie strategie:

  • udziałów obserwacji (ang. fractional instances) - rozważane są wszystkie możliwe podziały dla brakującej obserwacji i przypisywana jest im odpowiednia waga lub prawdopodobieństwo, w oparciu o zaobserwowany rozkład znanych obserwacji. Te same wagi są stosowane do predykcji wartości na podstawie drzewa z brakami danych.
  • podziałów zastępczych (ang. surrogate splits) - jeśli wynik podziału nie może być ustalony dla obserwacji z brakami, to używany jest podział zastępczy (pierwszy), jeśli i ten nie może zostać ustalony, to stosuje się kolejny. Kolejne podziały zastępcze są generowane tak, aby wynik podziału możliwie najbardziej przypominał podział właściwy.

4.8 Zalety i wady

4.8.1 Zalety

  • łatwe w interpretacji;
  • nie wymagają żmudnego przygotowania danych (brak standaryzacji, wprowadzania zmiennych binarnych, dopuszcza występowanie braków danych);
  • działa na obu typach zmiennych - jakościowych i ilościowych;
  • dopuszcza nieliniowość związku między zmienną wynikową a predyktorami;
  • odporny na odstępstwa od założeń;
  • pozwala na obsługę dużych zbiorów danych.

4.8.2 Wady

  • brak jawnej postaci zależności;
  • zależność struktury drzewa od użytego algorytmu;
  • przegrywa jakością predykcji z innymi metodami nadzorowanego uczenia maszynowego.

Przykład 4.1 Przykładem zastosowania drzew decyzyjnych będzie klasyfikacja irysów na podstawie długości i szerokości kielicha i płatka.

Przykładem zastosowania drzew decyzyjnych będzie klasyfikacja irysów na podstawie długości i szerokości kielicha i płatka.

library(tidyverse) 
library(rpart) # pakiet do tworzenia drzew typu CART
library(rpart.plot) # pakiet do rysowania drzew

Każde zadanie ucznia maszynowego zaczynamy od czyszczenia danych i odpowiedniego ich przygotowania ale w tym przypadku skupimy się jedynie na budowie, optymalizacji i ewaluacji modelu.

Podział zbioru na próbę uczącą i testową

set.seed(2019)
dt.train <- iris %>% 
    sample_frac(size = 0.7)
dt.test <- setdiff(iris, dt.train)
str(dt.train)
## 'data.frame':    105 obs. of  5 variables:
##  $ Sepal.Length: num  4.8 6.7 6.2 5.4 7.7 5 5.7 5 6.3 6.8 ...
##  $ Sepal.Width : num  3.4 3.3 2.2 3.9 2.6 2 3.8 3 3.4 3 ...
##  $ Petal.Length: num  1.9 5.7 4.5 1.3 6.9 3.5 1.7 1.6 5.6 5.5 ...
##  $ Petal.Width : num  0.2 2.1 1.5 0.4 2.3 1 0.3 0.2 2.4 2.1 ...
##  $ Species     : Factor w/ 3 levels "setosa","versicolor",..: 1 3 2 1 3 2 1 1 3 3 ...
str(dt.test)
## 'data.frame':    45 obs. of  5 variables:
##  $ Sepal.Length: num  4.4 5.4 4.8 4.3 5.7 5.1 5.2 5.2 5.2 4.9 ...
##  $ Sepal.Width : num  2.9 3.7 3 3 4.4 3.8 3.5 3.4 4.1 3.1 ...
##  $ Petal.Length: num  1.4 1.5 1.4 1.1 1.5 1.5 1.5 1.4 1.5 1.5 ...
##  $ Petal.Width : num  0.2 0.2 0.1 0.1 0.4 0.3 0.2 0.2 0.1 0.2 ...
##  $ Species     : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...

Budowa drzewa

Budowy drzewa dokonujemy za pomocą funkcji rpart pakietu rpart (Therneau and Atkinson 2018) stosując zapis formuły zależności. Drzewo zostanie zbudowane z uwzględnieniem kilku kryteriów zatrzymania:

  • minimalna liczebność węzła, który może zostać podzielony to 10 - ze względu na małą liczebność zbioru uczącego;
  • minimalna liczebność liścia to 5 - aby nie dopuścić do przeuczenia modelu;
  • maksymalna głębokość drzewa to 4 - aby nie dopuścić do przeuczenia modelu.
mod.rpart <- rpart(Species~., data = dt.train, 
                   control = rpart.control(minsplit = 10,
                                           minbucket = 5,
                                           maxdepth = 4))
summary(mod.rpart)
## Call:
## rpart(formula = Species ~ ., data = dt.train, control = rpart.control(minsplit = 10, 
##     minbucket = 5, maxdepth = 4))
##   n= 105 
## 
##           CP nsplit  rel error    xerror       xstd
## 1 0.51470588      0 1.00000000 1.1176471 0.06737554
## 2 0.39705882      1 0.48529412 0.4852941 0.06995514
## 3 0.02941176      2 0.08823529 0.1617647 0.04614841
## 4 0.01000000      3 0.05882353 0.1617647 0.04614841
## 
## Variable importance
##  Petal.Width Petal.Length Sepal.Length  Sepal.Width 
##           33           32           20           15 
## 
## Node number 1: 105 observations,    complexity param=0.5147059
##   predicted class=virginica   expected loss=0.647619  P(node) =1
##     class counts:    35    33    37
##    probabilities: 0.333 0.314 0.352 
##   left son=2 (35 obs) right son=3 (70 obs)
##   Primary splits:
##       Petal.Length < 2.6  to the left,  improve=35.03810, (0 missing)
##       Petal.Width  < 0.8  to the left,  improve=35.03810, (0 missing)
##       Sepal.Length < 5.45 to the left,  improve=25.60255, (0 missing)
##       Sepal.Width  < 3.35 to the right, improve=14.70881, (0 missing)
##   Surrogate splits:
##       Petal.Width  < 0.8  to the left,  agree=1.000, adj=1.000, (0 split)
##       Sepal.Length < 5.45 to the left,  agree=0.933, adj=0.800, (0 split)
##       Sepal.Width  < 3.35 to the right, agree=0.848, adj=0.543, (0 split)
## 
## Node number 2: 35 observations
##   predicted class=setosa      expected loss=0  P(node) =0.3333333
##     class counts:    35     0     0
##    probabilities: 1.000 0.000 0.000 
## 
## Node number 3: 70 observations,    complexity param=0.3970588
##   predicted class=virginica   expected loss=0.4714286  P(node) =0.6666667
##     class counts:     0    33    37
##    probabilities: 0.000 0.471 0.529 
##   left son=6 (37 obs) right son=7 (33 obs)
##   Primary splits:
##       Petal.Width  < 1.75 to the left,  improve=24.297670, (0 missing)
##       Petal.Length < 4.75 to the left,  improve=24.174190, (0 missing)
##       Sepal.Length < 5.75 to the left,  improve= 4.483555, (0 missing)
##       Sepal.Width  < 2.55 to the left,  improve= 3.793760, (0 missing)
##   Surrogate splits:
##       Petal.Length < 4.75 to the left,  agree=0.886, adj=0.758, (0 split)
##       Sepal.Length < 6.15 to the left,  agree=0.671, adj=0.303, (0 split)
##       Sepal.Width  < 2.65 to the left,  agree=0.671, adj=0.303, (0 split)
## 
## Node number 6: 37 observations,    complexity param=0.02941176
##   predicted class=versicolor  expected loss=0.1351351  P(node) =0.352381
##     class counts:     0    32     5
##    probabilities: 0.000 0.865 0.135 
##   left son=12 (31 obs) right son=13 (6 obs)
##   Primary splits:
##       Petal.Length < 4.95 to the left,  improve=4.0464980, (0 missing)
##       Petal.Width  < 1.35 to the left,  improve=1.0296010, (0 missing)
##       Sepal.Width  < 3.05 to the right, improve=0.2615519, (0 missing)
##       Sepal.Length < 5.95 to the left,  improve=0.1828101, (0 missing)
## 
## Node number 7: 33 observations
##   predicted class=virginica   expected loss=0.03030303  P(node) =0.3142857
##     class counts:     0     1    32
##    probabilities: 0.000 0.030 0.970 
## 
## Node number 12: 31 observations
##   predicted class=versicolor  expected loss=0.03225806  P(node) =0.2952381
##     class counts:     0    30     1
##    probabilities: 0.000 0.968 0.032 
## 
## Node number 13: 6 observations
##   predicted class=virginica   expected loss=0.3333333  P(node) =0.05714286
##     class counts:     0     2     4
##    probabilities: 0.000 0.333 0.667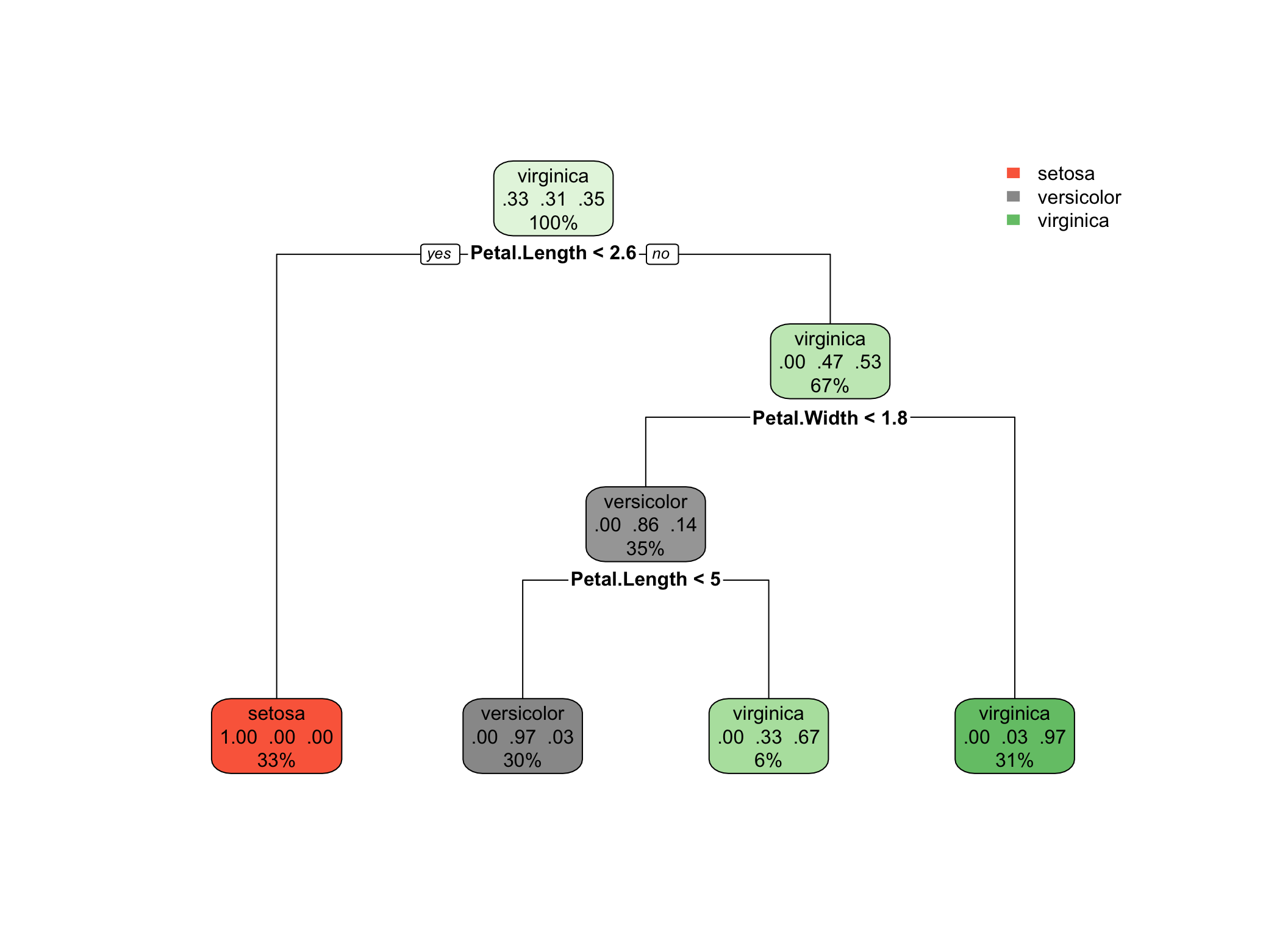
rpart.plot(mod.rpart)
Obraz drzewa klasyfikacyjnego.

Rysunek 4.2: Obraz drzewa klasyfikacyjnego.

Powyższy wykres przedstawia strukturę drzewa klasyfikacyjnego. Kolorami są oznaczone klasy, które w danym węźle dominują. Nasycenie barwy decyduje o sile tej dominacji. W każdym węźle podana jest klasa, do której najprawdopodobniej należą jego obserwacje. Ponadto podane są proporcje przynależności do klas zmiennej wynikowej oraz procent obserwacji zbioru uczącego należących do danego węzła. Pod każdym węzłem podana jest reguła podziału.

Przycinanie drzewa

Zanim przystąpimy do przycinania drzewa należy sprawdzić, jakie są zdolności generalizacyjne modelu. Oceny tej dokonujemy najczęściej sprawdzając macierz klasyfikacji.

pred.prob <- predict(mod.rpart, 
                     newdata = dt.test)
pred.prob[10:20,]
##    setosa versicolor  virginica
## 10      1  0.0000000 0.00000000
## 11      1  0.0000000 0.00000000
## 12      1  0.0000000 0.00000000
## 13      1  0.0000000 0.00000000
## 14      1  0.0000000 0.00000000
## 15      1  0.0000000 0.00000000
## 16      0  0.9677419 0.03225806
## 17      0  0.9677419 0.03225806
## 18      0  0.9677419 0.03225806
## 19      0  0.9677419 0.03225806
## 20      0  0.9677419 0.03225806
pred.class <- predict(mod.rpart, 
                      newdata = dt.test,
                      type = "class")
pred.class
##          1          2          3          4          5          6          7 
##     setosa     setosa     setosa     setosa     setosa     setosa     setosa 
##          8          9         10         11         12         13         14 
##     setosa     setosa     setosa     setosa     setosa     setosa     setosa 
##         15         16         17         18         19         20         21 
##     setosa versicolor versicolor versicolor versicolor versicolor versicolor 
##         22         23         24         25         26         27         28 
## versicolor versicolor versicolor versicolor versicolor versicolor versicolor 
##         29         30         31         32         33         34         35 
## versicolor versicolor versicolor versicolor  virginica  virginica  virginica 
##         36         37         38         39         40         41         42 
##  virginica  virginica  virginica  virginica  virginica  virginica  virginica 
##         43         44         45 
##  virginica  virginica  virginica 
## Levels: setosa versicolor virginica
tab <- table(predykcja = pred.class, obserwacja = dt.test$Species)
tab
##             obserwacja
## predykcja    setosa versicolor virginica
##   setosa         15          0         0
##   versicolor      0         17         0
##   virginica       0          0        13

Jak widać z powyższej tabeli, model całkiem dobrze radzi sobie z poprawną klasyfikacją obserwacji do odpowiednich kategorii.

W dalszej kolejności sprawdzimy, czy nie jest konieczne przycięcie drzewa. Jednym z kryteriów przycinania drzewa jest przycinanie ze względu na złożoność drzewa. W tym przypadku jest wyrażony parametrem cp. Istnieje powszechnie stosowana reguła jednego odchylenia standardowego, która mówi, że drzewo należy przyciąć wówczas, gdy błąd oszacowany na podstawie sprawdzianu krzyżowego (xerror), pierwszy raz zejdzie poniżej poziomu wyznaczonego przez najniższą wartość błędu powiększonego o odchylenie standardowe tego błędu (xstd). Na podstawie poniższej tabeli można ustalić, że poziomem odcięcia jest wartość \(0.16176+0.046148=0.207908\). Pierwszy raz błąd przyjmuje wartość mniejszą od \(0.16176\) po drugim podziale (nsplit=2). Temu poziomowi odpowiada cp o wartości \(0.029412\) i to jest złożoność drzewa, którą powinniśmy przyjąć do przycięcia drzewa.

printcp(mod.rpart)
## 
## Classification tree:
## rpart(formula = Species ~ ., data = dt.train, control = rpart.control(minsplit = 10, 
##     minbucket = 5, maxdepth = 4))
## 
## Variables actually used in tree construction:
## [1] Petal.Length Petal.Width 
## 
## Root node error: 68/105 = 0.64762
## 
## n= 105 
## 
##         CP nsplit rel error  xerror     xstd
## 1 0.514706      0  1.000000 1.11765 0.067376
## 2 0.397059      1  0.485294 0.48529 0.069955
## 3 0.029412      2  0.088235 0.16176 0.046148
## 4 0.010000      3  0.058824 0.16176 0.046148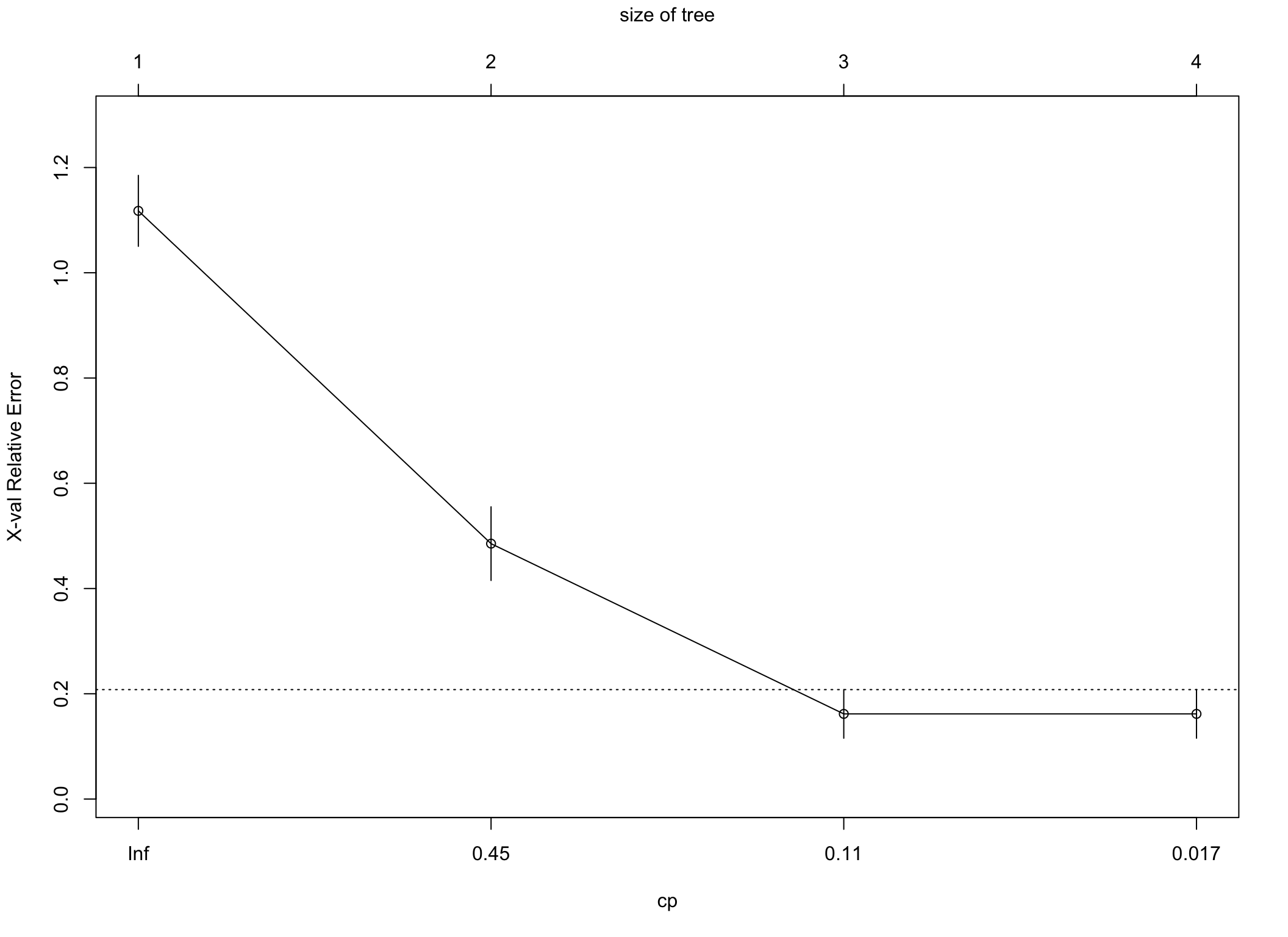
plotcp(mod.rpart)
Na wykresie błędów punkt odcięcia zaznaczony jest linią przerywaną

Rysunek 4.3: Na wykresie błędów punkt odcięcia zaznaczony jest linią przerywaną

Przycięte drzewo wygląda następująco:

mod.rpart2 <- prune(mod.rpart, cp = 0.029412)
summary(mod.rpart2)
## Call:
## rpart(formula = Species ~ ., data = dt.train, control = rpart.control(minsplit = 10, 
##     minbucket = 5, maxdepth = 4))
##   n= 105 
## 
##          CP nsplit  rel error    xerror       xstd
## 1 0.5147059      0 1.00000000 1.1176471 0.06737554
## 2 0.3970588      1 0.48529412 0.4852941 0.06995514
## 3 0.0294120      2 0.08823529 0.1617647 0.04614841
## 
## Variable importance
##  Petal.Width Petal.Length Sepal.Length  Sepal.Width 
##           34           31           20           15 
## 
## Node number 1: 105 observations,    complexity param=0.5147059
##   predicted class=virginica   expected loss=0.647619  P(node) =1
##     class counts:    35    33    37
##    probabilities: 0.333 0.314 0.352 
##   left son=2 (35 obs) right son=3 (70 obs)
##   Primary splits:
##       Petal.Length < 2.6  to the left,  improve=35.03810, (0 missing)
##       Petal.Width  < 0.8  to the left,  improve=35.03810, (0 missing)
##       Sepal.Length < 5.45 to the left,  improve=25.60255, (0 missing)
##       Sepal.Width  < 3.35 to the right, improve=14.70881, (0 missing)
##   Surrogate splits:
##       Petal.Width  < 0.8  to the left,  agree=1.000, adj=1.000, (0 split)
##       Sepal.Length < 5.45 to the left,  agree=0.933, adj=0.800, (0 split)
##       Sepal.Width  < 3.35 to the right, agree=0.848, adj=0.543, (0 split)
## 
## Node number 2: 35 observations
##   predicted class=setosa      expected loss=0  P(node) =0.3333333
##     class counts:    35     0     0
##    probabilities: 1.000 0.000 0.000 
## 
## Node number 3: 70 observations,    complexity param=0.3970588
##   predicted class=virginica   expected loss=0.4714286  P(node) =0.6666667
##     class counts:     0    33    37
##    probabilities: 0.000 0.471 0.529 
##   left son=6 (37 obs) right son=7 (33 obs)
##   Primary splits:
##       Petal.Width  < 1.75 to the left,  improve=24.297670, (0 missing)
##       Petal.Length < 4.75 to the left,  improve=24.174190, (0 missing)
##       Sepal.Length < 5.75 to the left,  improve= 4.483555, (0 missing)
##       Sepal.Width  < 2.55 to the left,  improve= 3.793760, (0 missing)
##   Surrogate splits:
##       Petal.Length < 4.75 to the left,  agree=0.886, adj=0.758, (0 split)
##       Sepal.Length < 6.15 to the left,  agree=0.671, adj=0.303, (0 split)
##       Sepal.Width  < 2.65 to the left,  agree=0.671, adj=0.303, (0 split)
## 
## Node number 6: 37 observations
##   predicted class=versicolor  expected loss=0.1351351  P(node) =0.352381
##     class counts:     0    32     5
##    probabilities: 0.000 0.865 0.135 
## 
## Node number 7: 33 observations
##   predicted class=virginica   expected loss=0.03030303  P(node) =0.3142857
##     class counts:     0     1    32
##    probabilities: 0.000 0.030 0.970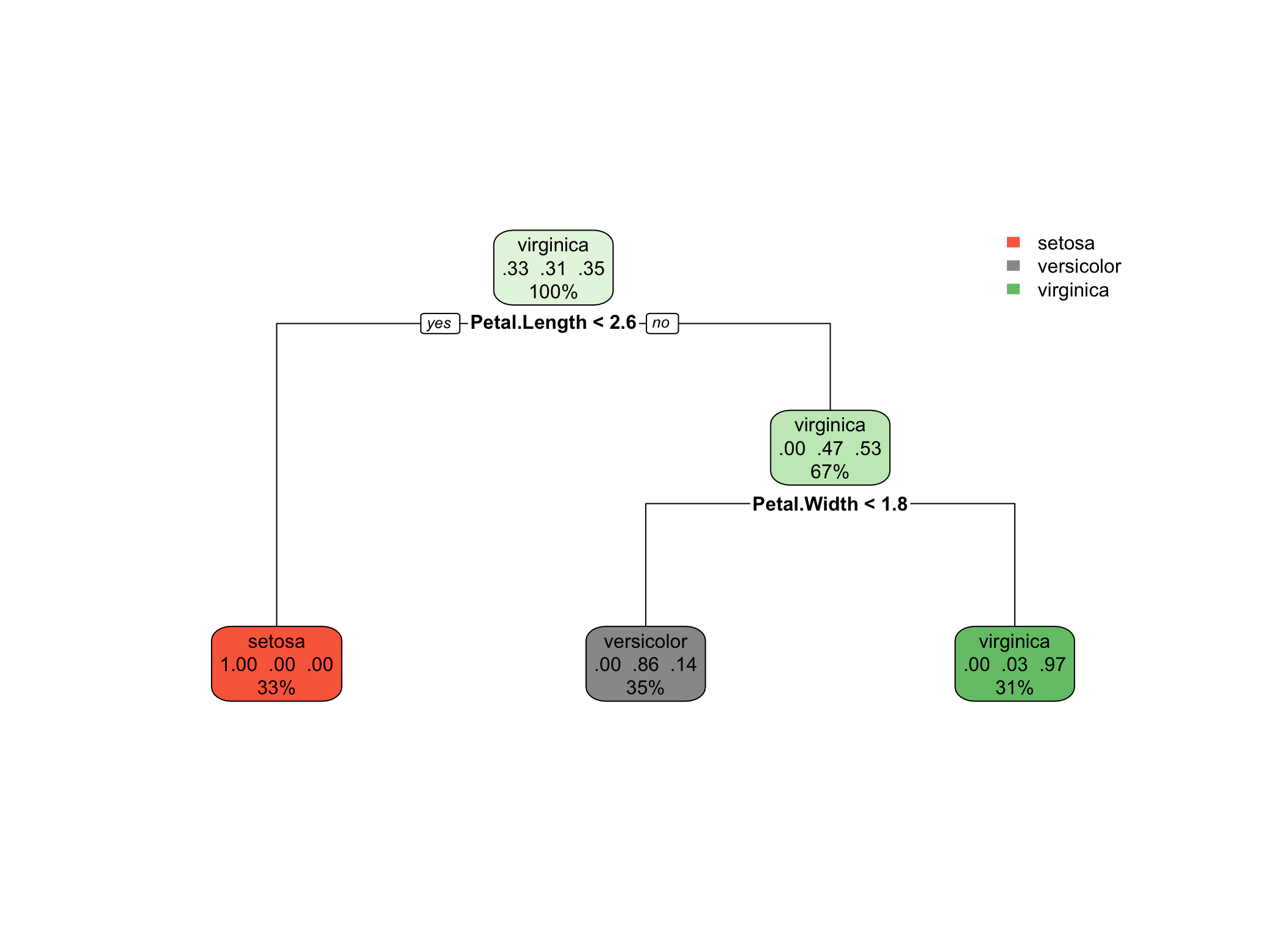
rpart.plot(mod.rpart2)
Drzewo klasyfikacyjne po przycięciu

Rysunek 4.4: Drzewo klasyfikacyjne po przycięciu

Ocena dopasowania modelu

Na koniec budowy modelu należy sprawdzić jego jakość na zbiorze testowym.

pred.class2 <- predict(mod.rpart2,
                       newdata = dt.test,
                       type = "class")
tab2 <- table(predykcja = pred.class2, obserwacja = dt.test$Species)
tab2
##             obserwacja
## predykcja    setosa versicolor virginica
##   setosa         15          0         0
##   versicolor      0         17         0
##   virginica       0          0        13

Mimo przycięcia drzewa, klasyfikacja pozostaje na niezmienionym poziomie. Odsetek poprawnych klasyfikacji możemy oszacować za pomocą

round(sum(diag(tab2))/sum(tab2)*100,1)
## [1] 100

4.9 Inne algorytmy budowy drzew decyzyjnych implementowane w R

Oprócz najbardziej znanego algorytmu CART implementowanego w postaci funkcji pakietu rpart, istnieją również inne algorytmy, które znalazły swoje implementacje w R. Są to:

  • CHAID13 - algorytm przeznaczony do budowy drzew klasyfikacyjnych, gdzie zarówno zmienna wynikowa, jak i zmienne niezależne muszą być ze skali jakościowej. Główną różnicą w stosunku do drzew typu CART jest sposób budowy podziałów, oparty na teście niezależności \(\chi^2\) Pearsona. Wyboru reguły podziału dokonuje się poprzez testowanie niezależności zmiennej niezależnej z predyktorami. Reguła o największej wartości statystyki \(\chi^2\) jest stosowana w pierwszej kolejności. Implementacja tego algorytmu znajduje się w pakiecie CHAID14 (funkcja do tworzenia drzewa o tej samej nazwie chaid) (Team 2015).
  • Ctree15 - algorytm zbliżony zasadą działania do CHAID, ponieważ również wykorzystuje testowanie do wyboru reguły podziału. Różni się jednak tym, że może być stosowany do zmiennych dowolnego typu oraz tym, że może być zarówno drzewem klasyfikacyjnym jak i regresyjnym. Implementację R-ową można znaleźć w pakietach party (Hothorn, Hornik, and Zeileis 2006) lub partykit (Hothorn and Zeileis 2015) - funkcją do tworzenia modelu jest ctree.
  • C4.5 - algorytm stworzony przez Quinlan (1993) w oparciu, o również jego autorstwa, algorytm ID3. Służy jedynie do zadań klasyfikacyjnych. W dużym uproszczeniu, dobór reguł podziału odbywa się na podstawie przyrostu informacji (patrz Reguły podziału). W przeciwieństwie do pierwotnego algorytmu ID3, C4.5 nie raczej nie przeucza drzew. Implementacja R-owa znajduje się w pakiecie RWeka (Hornik, Buchta, and Zeileis 2009) - funkcja do budowy drzewa to J48.
  • C5.0 - kolejny algorytm autorstwa Kuhn and Quinlan (2018) jest usprawnieniem algorytmu C4.5, generującym mniejsze drzewa automatycznie przycinane na podstawie złożoności drzewa. Służy jedynie do zadań klasyfikacyjnych. Jest szybszy od poprzednika i pozwala na zastosowanie metody boosting16. Implementacja R-owa znajduje się w pakiecie C50, a funkcja do budowy drzewa to C5.0.

Przykład 4.2 W celu porównania wyników klasyfikacji na podstawie drzew decyzyjnych o różnych algorytmach, zostaną nauczone modele w oparciu o funkcje ctree, J48 i C5.0 dla tego samego zestawu danych co w przykładzie wcześniejszym 4.1.

  • Drzewo ctree

Na początek ustalamy parametry ograniczające rozrost drzewa podobne jak w poprzednim przykładzie.

library(partykit)
tree2 <- ctree(Species~., data = dt.train,
               control = ctree_control(minsplit = 10,
                                       minbucket = 5,
                                       maxdepth = 4))
tree2
## 
## Model formula:
## Species ~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width
## 
## Fitted party:
## [1] root
## |   [2] Petal.Length <= 1.9: setosa (n = 35, err = 0.0%)
## |   [3] Petal.Length > 1.9
## |   |   [4] Petal.Width <= 1.7
## |   |   |   [5] Petal.Length <= 4.9: versicolor (n = 31, err = 3.2%)
## |   |   |   [6] Petal.Length > 4.9: virginica (n = 6, err = 33.3%)
## |   |   [7] Petal.Width > 1.7: virginica (n = 33, err = 3.0%)
## 
## Number of inner nodes:    3
## Number of terminal nodes: 4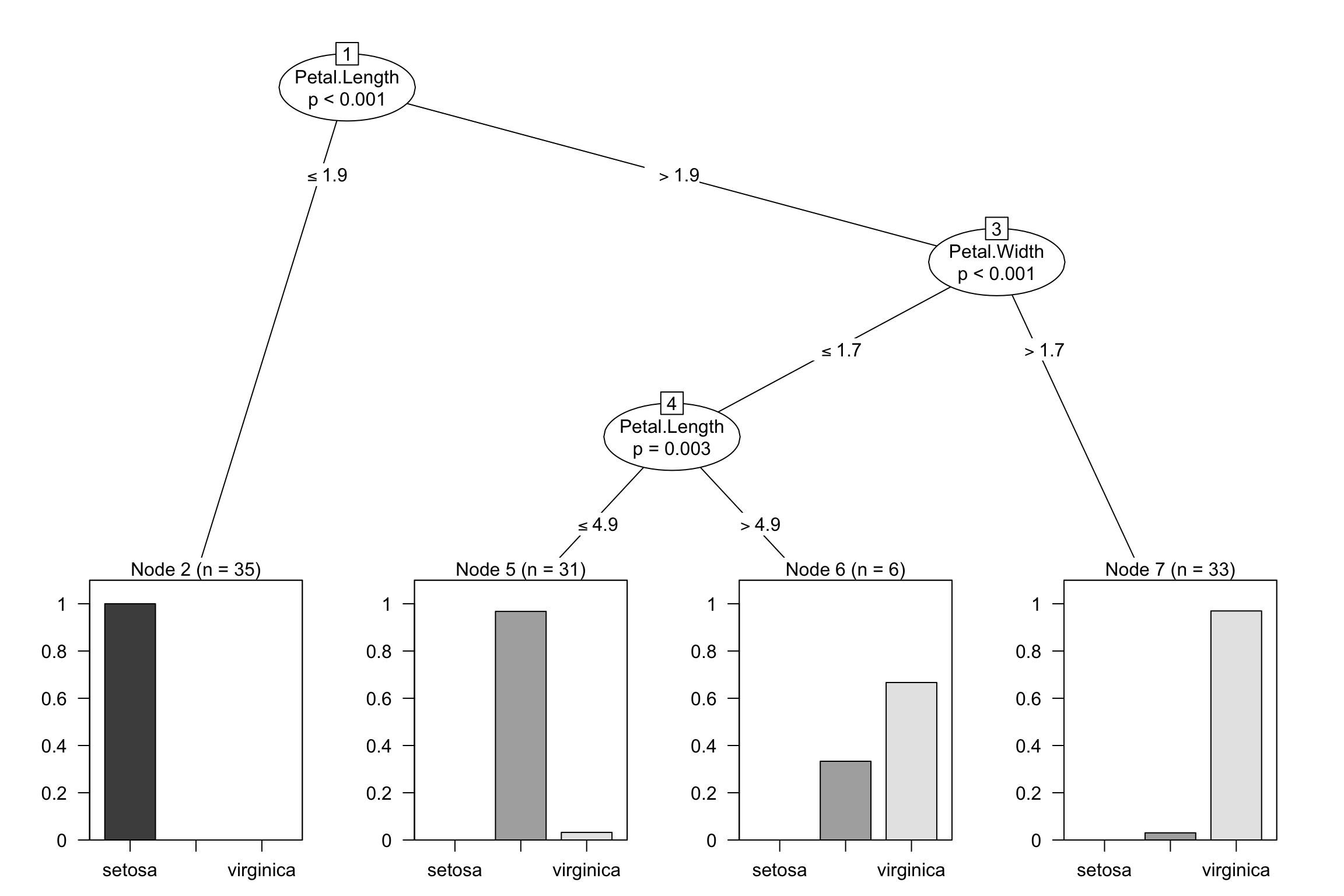
plot(tree2)
Wykres drzewa decyzyjnego zbudowanego metodą ctree

Rysunek 4.5: Wykres drzewa decyzyjnego zbudowanego metodą ctree

Wydaje się, że drzewo nie jest optymalne, ponieważ w węźle 6 obserwacje z grup versicolor i virginica są nieco pomieszane. Ostateczne oceny dokonujemy na podstawie próby testowej.

pred2 <- predict(tree2, newdata = dt.test)
tab <- table(predykcja = pred2, obserwacja = dt.test$Species)
tab
##             obserwacja
## predykcja    setosa versicolor virginica
##   setosa         15          0         0
##   versicolor      0         17         0
##   virginica       0          0        13

Dopiero ocena jakości klasyfikacji na podstawie próby testowej pokazuje, że model zbudowany za pomocą ctree daje podobną precyzję jak rpart przycięty.

  • Drzewo J48

W tym przypadku model sam poszukuje optymalnego rozwiązania przycinając się automatycznie.

library(RWeka)
tree3 <- J48(Species~., data = dt.train)
tree3
## J48 pruned tree
## ------------------
## 
## Petal.Width <= 0.6: setosa (35.0)
## Petal.Width > 0.6
## |   Petal.Width <= 1.7
## |   |   Petal.Length <= 4.9: versicolor (31.0/1.0)
## |   |   Petal.Length > 4.9
## |   |   |   Petal.Width <= 1.5: virginica (3.0)
## |   |   |   Petal.Width > 1.5: versicolor (3.0/1.0)
## |   Petal.Width > 1.7: virginica (33.0/1.0)
## 
## Number of Leaves  :  5
## 
## Size of the tree :   9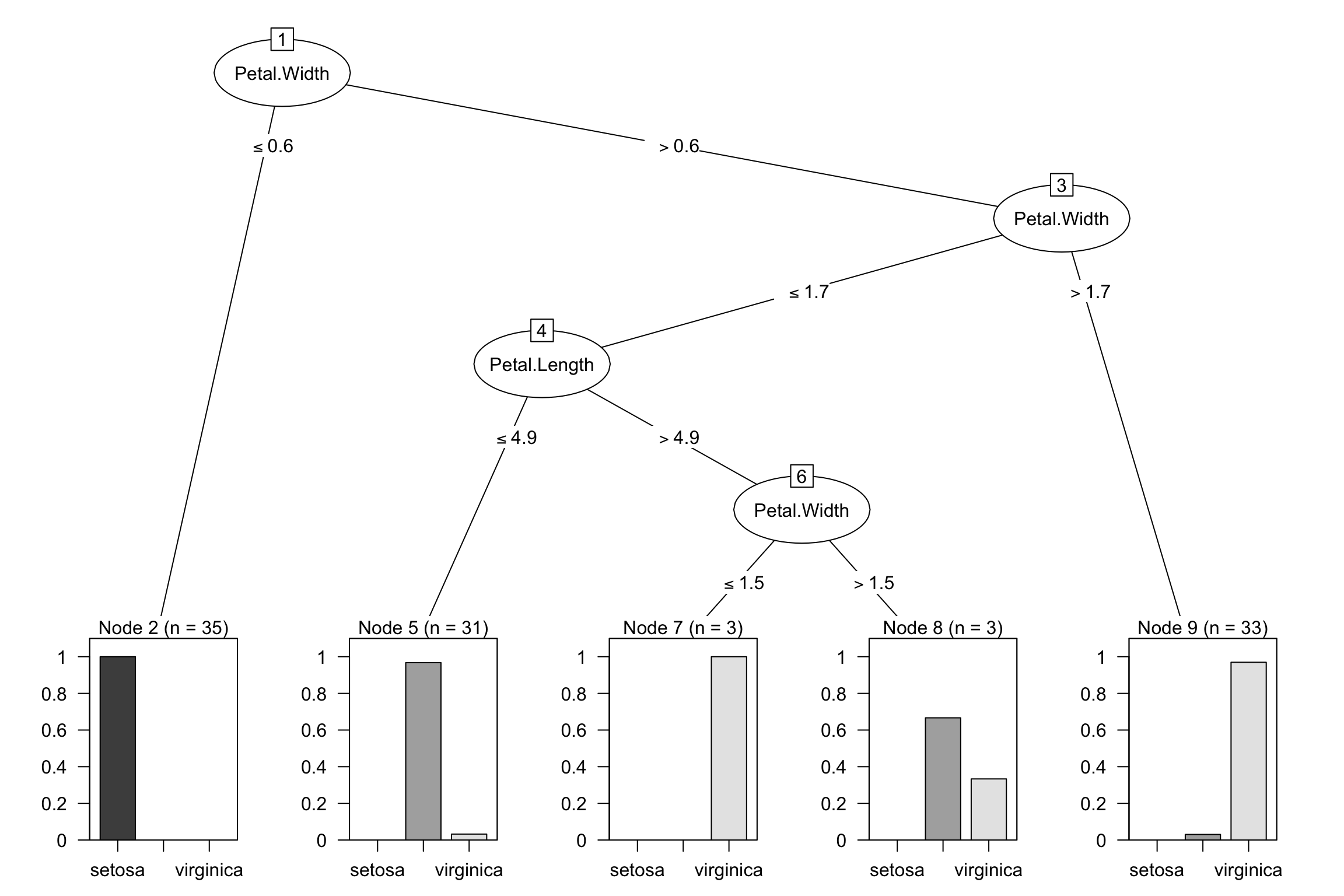
plot(tree3)
Wykres drzewa decyzyjnego zbudowanego metodą J48

Rysunek 4.6: Wykres drzewa decyzyjnego zbudowanego metodą J48

Drzewo jest nieco bardziej rozbudowane niż tree2 i mod.rpart2.

summary(tree3)
## 
## === Summary ===
## 
## Correctly Classified Instances         102               97.1429 %
## Incorrectly Classified Instances         3                2.8571 %
## Kappa statistic                          0.9571
## Mean absolute error                      0.0331
## Root mean squared error                  0.1286
## Relative absolute error                  7.4482 %
## Root relative squared error             27.2918 %
## Total Number of Instances              105     
## 
## === Confusion Matrix ===
## 
##   a  b  c   <-- classified as
##  35  0  0 |  a = setosa
##   0 32  1 |  b = versicolor
##   0  2 35 |  c = virginica

Podsumowanie dopasowania drzewa na próbie uczącej jest bardzo dobre, bo poprawnych klasyfikacji jest ponad 97%. Oceny dopasowania i tak dokonujemy na zbiorze testowym.

pred3 <- predict(tree3, newdata = dt.test)
tab <- table(predykcja = pred3, obserwacja = dt.test$Species)
tab
##             obserwacja
## predykcja    setosa versicolor virginica
##   setosa         15          0         0
##   versicolor      0         17         0
##   virginica       0          0        13

Otrzymujemy identyczną macierz klasyfikacji jak w poprzednich przypadkach.

  • Drzewo C50

Tym razem również nie trzeba ustawiać parametrów drzewa, ponieważ algorytm działa tak aby zapobiec rozrostowi drzewa przy jednoczesnej wysokiej poprawności klasyfikacji.

library(C50)
tree4 <- C5.0(Species~., data = dt.train)
summary(tree4)
## 
## Call:
## C5.0.formula(formula = Species ~ ., data = dt.train)
## 
## 
## C5.0 [Release 2.07 GPL Edition]      Tue Apr 23 09:05:07 2024
## -------------------------------
## 
## Class specified by attribute `outcome'
## 
## Read 105 cases (5 attributes) from undefined.data
## 
## Decision tree:
## 
## Petal.Length <= 1.9: setosa (35)
## Petal.Length > 1.9:
## :...Petal.Width > 1.7: virginica (33/1)
##     Petal.Width <= 1.7:
##     :...Petal.Length <= 4.9: versicolor (31/1)
##         Petal.Length > 4.9: virginica (6/2)
## 
## 
## Evaluation on training data (105 cases):
## 
##      Decision Tree   
##    ----------------  
##    Size      Errors  
## 
##       4    4( 3.8%)   <<
## 
## 
##     (a)   (b)   (c)    <-classified as
##    ----  ----  ----
##      35                (a): class setosa
##            30     3    (b): class versicolor
##             1    36    (c): class virginica
## 
## 
##  Attribute usage:
## 
##  100.00% Petal.Length
##   66.67% Petal.Width
## 
## 
## Time: 0.0 secs

Otrzymujemy identyczne drzewo jak w przypadku zastosowania algorytmu ctree.

plot(tree4)
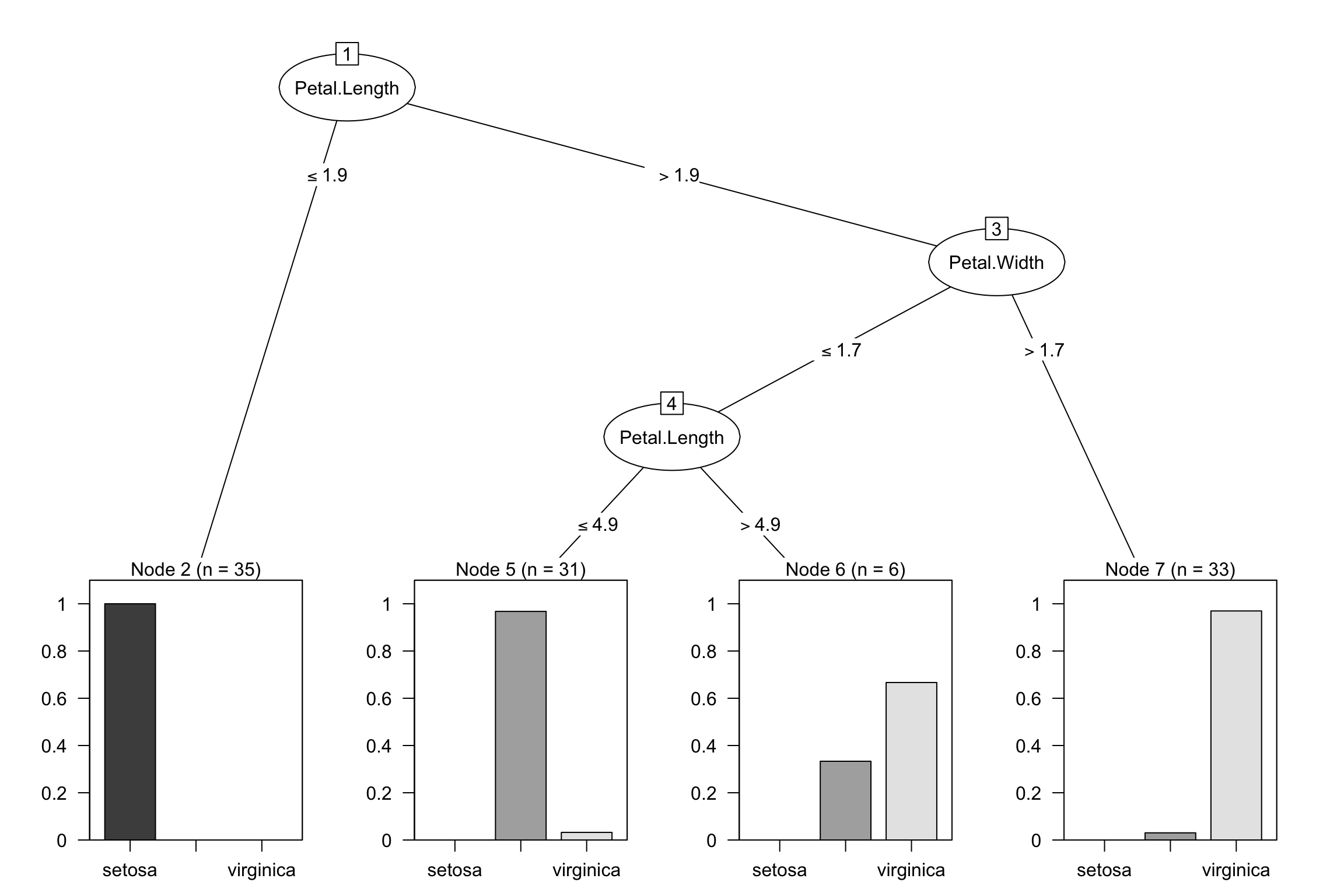
Wykres drzewa decyzyjnego zbudowanego metodą C5.0

Rysunek 4.7: Wykres drzewa decyzyjnego zbudowanego metodą C5.0

Dla pewności przeprowadzimy sprawdzenie na zbiorze testowym.

pred4 <- predict(tree4, newdata = dt.test)
tab <- table(predykcja = pred4, obserwacja = dt.test$Species)
tab
##             obserwacja
## predykcja    setosa versicolor virginica
##   setosa         15          0         0
##   versicolor      0         17         0
##   virginica       0          0        13

Bibliografia

———. 1998. “Arcing Classifier (with Discussion and a Rejoinder by the Author).” Ann. Statist. 26 (3): 801–49. https://doi.org/10.1214/aos/1024691079.
Hornik, Kurt, Christian Buchta, and Achim Zeileis. 2009. “Open-Source Machine Learning: R Meets Weka.” Computational Statistics 24 (2): 225–32. https://doi.org/10.1007/s00180-008-0119-7.
Hothorn, Torsten, Kurt Hornik, and Achim Zeileis. 2006. “Unbiased Recursive Partitioning: A Conditional Inference Framework.” Journal of Computational and Graphical Statistics 15 (3): 651–74. https://doi.org/10.1198/106186006X133933.
Hothorn, Torsten, and Achim Zeileis. 2015. “Partykit: A Modular Toolkit for Recursive Partytioning in r.” Journal of Machine Learning Research 16: 3905–9. http://jmlr.org/papers/v16/hothorn15a.html.
Kuhn, Max, and Ross Quinlan. 2018. C50: C5.0 Decision Trees and Rule-Based Models. https://CRAN.R-project.org/package=C50.
Quinlan, J Ross. 1993. C4. 5: Programs for Machine Learning. Morgan Kaufmann.
Team, The FoRt Student Project. 2015. CHAID: CHi-Squared Automated Interaction Detection.
Therneau, Terry, and Beth Atkinson. 2018. Rpart: Recursive Partitioning and Regression Trees. https://CRAN.R-project.org/package=rpart.

  1. wyglądem przypomina odwrócone drzewo, stąd nazwa↩︎

  2. prawie wszystkie są w jednej klasie↩︎

  3. Chi-square automatic interaction detection↩︎

  4. brak w oficjalnej dystrybucji CRAN↩︎

  5. Conditional Inference Trees↩︎

  6. budowa klasyfikatora w oparciu o proces iteracyjny, w którym kolejne w kolejnych iteracjach budowane są proste drzewa i przypisywane są im wagi - im gorszy klasyfikator, tym większa waga - po to aby nauczyć drzewo klasyfikować “trudne” przypadki↩︎