11 Uogólnione modele addytywne

Modele liniowe, jako techniki klasyfikacji i regresji, mają niewątpliwą zaletę - jawna postać zależności pomiędzy predyktorami i zmienną wynikową. Często w rzeczywistości tak uproszczony model nie potrafi oddać złożoności natury badanego zjawiska. Dlatego powstał pomysł aby w miejsce kombinacji liniowej predyktorów wstawić kombinację liniową ich funkcji, czyli \[\begin{equation} \E(Y|X)=f(X) = \sum_{i=1}^M\beta_mh_m(X), \tag{11.1} \end{equation}\] gdzie \(h_m:\mathbb{R}^d\to\mathbb{R}\) nazywana często funkcją bazową (ang. linear basis expansion). Wówczas w zależności od postaci funkcji bazowej otrzymujemy modele z różnymi poziomami elastyczności:

• gdy \(h_m(X)=X_m,\ m=1,\ldots,M\), to otrzymujemy model liniowy;
• gdy \(h_m(X)=X_j^2\) lub \(h_m(X)=X_jX_k\), to otrzymujemy struktury wielomianowe, charakteryzujące się większą elastycznością modelu;
• gdy \(h_m(X)=\log X_j\) lub \(h_m(X)=\sqrt{X_j}\), to uzyskujemy nieliniowość czynników wchodzących w skład kombinacji liniowej (11.1);
• dopuszczalne są również kawałkami liniowe funkcje postaci \(h_m(X)= I(l_m\leq X_k <u_m)\), gdzie \(I\) jest funkcją charakterystyczną (ang. indicator) przedziału \([l_m,u_m)\).

Zbiory wszystkich funkcji bazowych definiowanych w ten sposób tworzy słownik funkcji bazowych \(\mathcal{D}\). Aby kontrolować złożoność modeli, mając do dyspozycji tak zasobny słownik, wprowadza się następujące podejścia:

• ogranicza się klasę dostępnych funkcji bazowych \[\begin{equation} f(X) = \sum_{j=1}^df_j(X_j)=\sum_{j=1}^d\sum_{m=1}^{M_j}\beta_{jm}h_{jm}(X_j), \end{equation}\]
• włącza się do modelu jedynie te funkcje ze słownika \(\mathcal{D}\), które istotnie poprawiają dopasowanie modelu,
• używa się metod penalizowanych, czyli dopuszcza się stosowanie wszystkich funkcji bazowych ze słownika \(\mathcal{D}\), ale współczynniki przy nich stojące są ograniczane.

11.1 Przypadek jednowymiarowy

Dla uproszczenia rozważań przyjmiemy, że \(X\) jest jednowymiarowe.

Rysunek 11.1: Przykładowe zastosowanie kilku rodzajów funkcji bazowych. Wykres w lewym górnym rogu powstał ze stałych na przedziałach, wykres w górnym prawym rogu powstał z liniowych funkcji bazowych na przedzialach, w lewym dolnym rogu model powstał również z liniowych funkcji bazowych na przedzialach ale z założeniem ciągłości, a prawym dolnym rogu powstał z zastosowania funcji bazowej \(\max(X-\xi_1,0)\)

Rysunek 11.2: Kolejne wykresy przedstawiają coraz bardziej gładkie modele będące efektem dodawania wielomianów trzeciego stopnia na przedziałach. Na każdym kolejnym modelu mymuszone zostały silniejsze założenia dotyczące gładkości

Przykładowo sześcienny splajn²⁰ dla dwóch punków węzłowych składa się z następujących funkcji bazowych

\[\begin{gather} h_1(X)=1,\quad h_3(X)=X^2,\quad h_5(X)=(X-\xi_1)_+^3\\ h_2(X)=X,\quad h_4(X)=X^3,\quad h_6(X)=(X-\xi_2)_+^3. \end{gather}\]

Zachowanie wielomianów poza punktami węzłowymi jest czasami bardzo dziwne. Zdarza się, że charakteryzują się tam dużą zmiennością. Dlatego wprowadza się takie splajny aby w obszarach brzegowych zachowywały się przewidywalnie. Naturalny splajn sześcienny zakłada liniowość modelu poza węzłami brzegowymi. Dla \(K\) węzłów naturalny splajn sześcienny składa się z następujących funkcji bazowych

\[\begin{gather} N_1(X)=1,\quad N_2(X)=X,\quad N_{k+2}(X)=d_k(X)-d_{K-1}(X), \end{gather}\] gdzie \(d_k(X)=\frac{(X-\xi_k)^3_+-(X-\xi_K)^3_+}{\xi_K-\xi_k}.\)

Estymacji parametrów modelu dokonujemy metodą najmniejszych kwadratów, minimalizując \[\begin{equation} RSS(f,\lambda) = \sum_{i=1}^N(y_i-f(x_i))^2+\lambda\int(f''(t))^2dt, \end{equation}\] gdzie \(\lambda\) jest parametrem wygładzania. Pierwsze wyrażenie po prawej stronie to ocena dopasowania, a drugie to kara za krzywoliniowość. Dla naturalnego splajna \[\begin{equation} f(x)=\sum_{j=1}^NN_j(x)\beta_j \end{equation}\] minimalizujemy \[\begin{equation} RSS(\beta, \lambda)=(\boldsymbol y -\boldsymbol N\beta)'(\boldsymbol y-\boldsymbol N\beta)+\lambda\beta'\boldsymbol \Omega \beta, \end{equation}\] gdzie \(\{\boldsymbol N\}_{ij}= N_j(x_i)\) i \(\{\boldsymbol \Omega\}_{jk}=\int N''_j(t)N''_k(t)dt\). Rozwiązaniem zaganienia minimalizacji \(RSS(\beta,\lambda)\) jest \[\begin{equation} \hat{\beta}=((\boldsymbol N'\boldsymbol N)+\lambda\boldsymbol \Omega)^{-1}\boldsymbol N'\boldsymbol y. \end{equation}\]

11.2 Przypadek wielowymiarowy

W przypadku gdy \(X\in \mathbb{R}^d\) poszukujemy takiej \(d\)-wymiarowej regresji \(f(x)\), która będzie minimalizowała wyrażenie \[\begin{equation} \min_f\sum_{i=1}^N(y_i-f(x_i))^2+\lambda J(f), \end{equation}\] gdzie \(J\) jest odpowiednią funkcją wyrażającą krzywoliniowość modelu. Dla \(X\in \mathbb{R}^2\) przyjmuje postać \[\begin{equation} J(f)=\iint_{\mathbb{R}^2}\left[\left(\frac{\partial^2 f(x)}{\partial^2 x_1}\right)^2+2\left(\frac{\partial^2 f(x)}{\partial x_1\partial x_2}\right)^2+ \left(\frac{\partial^2 f(x)}{\partial^2 x_2}\right)^2\right]dx_1dx_2. \end{equation}\] Rozwiązanie przyjmuje postać \[\begin{equation} f(x) = \beta_0+\beta'x+\sum_{i=1}^N \alpha_ih_i(x), \end{equation}\] gdzie \(h_i(x)=||x-x_j||^2\log||x-x_j||\).

11.3 Uogólnione modele addytywne

Przez uogólnione modele addytywne (ang. Generalized Additive Models) rozumiemy klasę modeli, które poprzez funkcję łączącą, opisują warunkową wartość zmiennej wynikowej w następujący sposób \[\begin{equation} g(\E(Y|X))=g(\mu(X))=\alpha+f_1(X_1)+\dots+f_d(X_d), \end{equation}\] gdzie \(g\) jest funkcją łączącą. Najczęściej stosowanymi funkcjami łączącymi są:

• \(g(\mu)=\mu\) - stosowana w modelach, gdy zmienna wynikowa ma rozkład normalny;
• \(g(\mu)=\logit\mu\) - stosowana, gdy zmienna wynikowa ma rozkład dwumianowy;
• \(g(\mu)=\probit\mu\) - stosowana również w przypadku gdy zmienna ma rozkład dwumianowy, a \(\Phi^{-1}\) oznacza odwrotność dystrybuanty standaryzowanego rozkładu normalnego;
• \(g(\mu)=\log\mu\) - stosowana, gdy zmienna wynikowa jest zmienną typu zliczeniowego (rozkład Poissona).

11.3.1 Algorytm uczenia modelu GAM

Algorytm uczenia wstecznego (ang. backfitting) przebiega wg następujących kroków:

1. Ustalamy wstępne oszacowania na \(\alpha=\bar{y}\) i \(\hat{f}_j=0\).
2. Dla \(j=1,\ldots,d,1,\ldots,d,1,\ldots\) powtarzamy szacowanie \[\begin{align} \hat{f}_j\leftarrow &\mathcal{S}_j\left[(y_i-\hat{\alpha}-\sum_{k\neq j}\hat{f}_k(x_{ik}))^N_1\right],\\ \hat{f}_j\leftarrow &\hat{f}_j-\frac{1}{N}\sum_{i=1}^N\hat{f}_j(x_{ij}) \end{align}\] dopóki \(\hat{f}_j\) osiągnie zbieżność. Funkcja \(\mathcal{S}_j\left[(y_i-\hat{\alpha}-\sum_{k\neq j}\hat{f}_k(x_{ik}))^N_1\right]\) jest jednowymiarowym sześciennym splajnem o \(N\) węzłach. W jej miejsce można przyjąć również inne funkcje, takie jak: jednowymiarowe lokalne regresje wielomianowe (ang. LOESS - locally estimated scatterplot smoothing), regresje liniowe, wielomianowe.

Przykład 11.1 Dla zilustrowania zasady działania uogólnionych modeli addytywnych przeprowadzimy analizę stężenia ozonu (\(O_3\)) w zależności od wybranych parametrów meteorologicznych. Do zbudowania modelu GAM wykorzystamy funkcję gam pakietu mgcv (Wood 2003).

library(faraway)
head(ozone)

##   O3   vh wind humidity temp  ibh dpg ibt vis doy
## 1  3 5710    4       28   40 2693 -25  87 250  33
## 2  5 5700    3       37   45  590 -24 128 100  34
## 3  5 5760    3       51   54 1450  25 139  60  35
## 4  6 5720    4       69   35 1568  15 121  60  36
## 5  4 5790    6       19   45 2631 -33 123 100  37
## 6  4 5790    3       25   55  554 -28 182 250  38

library(mgcv)
mod.gam <- gam(O3~s(temp, bs = "cr", m = 2)+s(ibh)+s(ibt), data = ozone)
summary(mod.gam)

## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## O3 ~ s(temp, bs = "cr", m = 2) + s(ibh) + s(ibt)
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  11.7758     0.2382   49.44   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##           edf Ref.df      F  p-value    
## s(temp) 3.357  4.216 20.758  < 2e-16 ***
## s(ibh)  4.171  5.072  7.344 1.73e-06 ***
## s(ibt)  2.111  2.729  1.403    0.212    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.708   Deviance explained = 71.7%
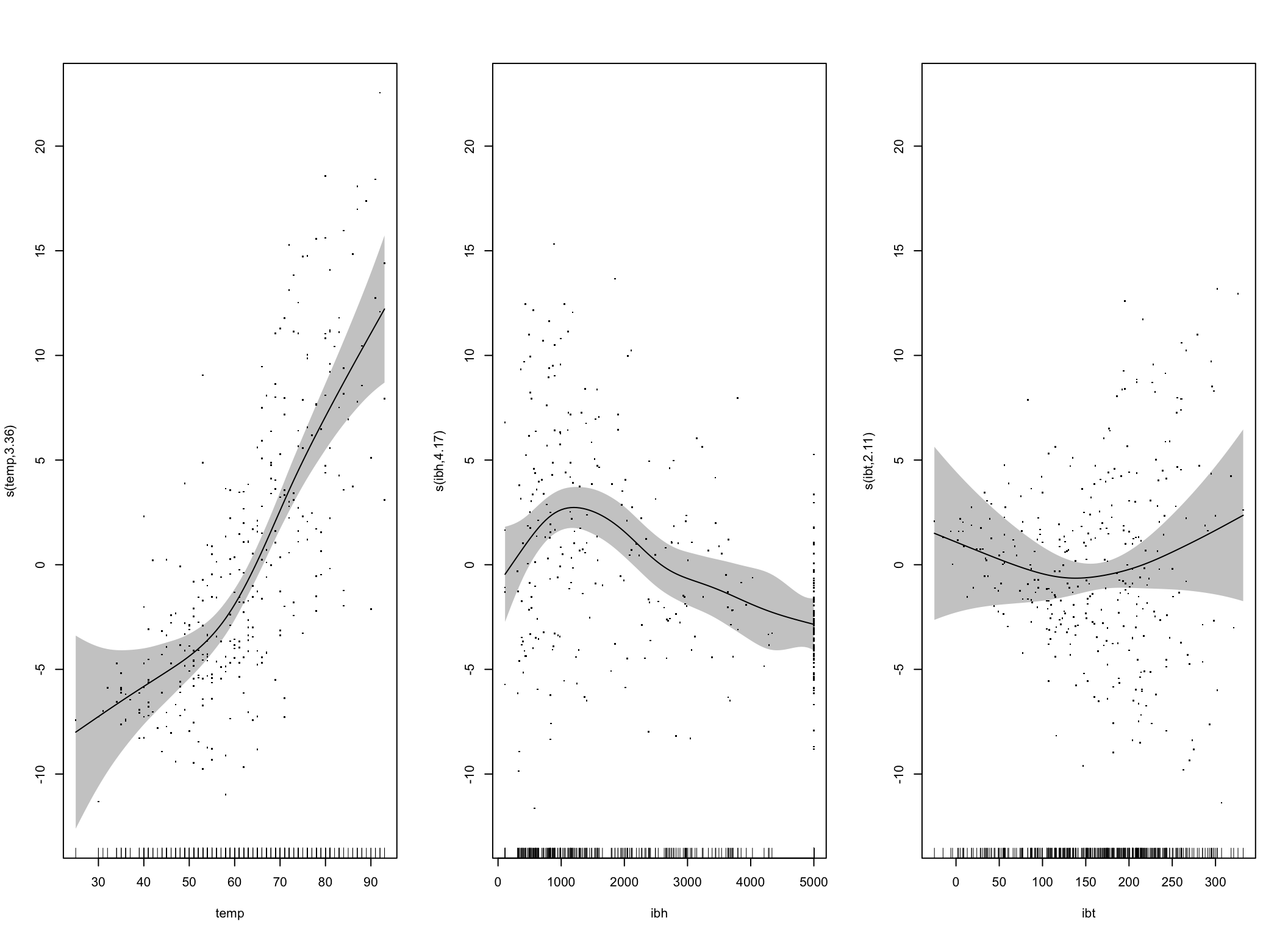
## GCV = 19.348  Scale est. = 18.724    n = 330

W powyższym modelu użyto splajnów jako funkcji \(f_i\). W przypadku zmiennej temp był to sześcienny splajn z regularyzacją w postaci ciągłości drugiej pochodnej, a pozostałe są prostymi splajnami. Dopasowanie modelu sięga 71.7% a wartość uogólnionego sprawdzianu krzyżowego 19.35.

Poniższy wykres pokazuje rodzaje transformacji użyte przy dopasowaniu modelu.

par(mfrow = c(1,3))
plot(mod.gam, shade = T, residuals = T)

par(mfrow=c(1,1))

Bibliografia

Wood, S. N. 2003. “Thin-Plate Regression Splines.” Journal of the Royal Statistical Society (B) 65 (1): 95–114.

---

20. czyli funkcja łączona↩︎