8 Filtry morfologiczne
Omawiając filtr medianowy , zauważyliśmy, że ten typ filtra może w pewien sposób zmieniać struktury obrazów dwuwymiarowych. Rysunek 8.1 ilustruje, w jaki sposób wypełniane są otwory o określonym rozmiarze oraz usuwane małe struktury, takie jak pojedyncze kropki lub cienkie linie. Filtr medianowy reaguje więc wybiórczo na lokalny kształt struktur obrazu, co jest właściwością, która może być przydatna do innych celów, jeśli można ją stosować nie tylko losowo, ale w sposób kontrolowany. Zmienianie lokalnej struktury w przewidywalny sposób jest właśnie tym, co potrafią robić filtry “morfologiczne”, na których skupiamy się w tym rozdziale.
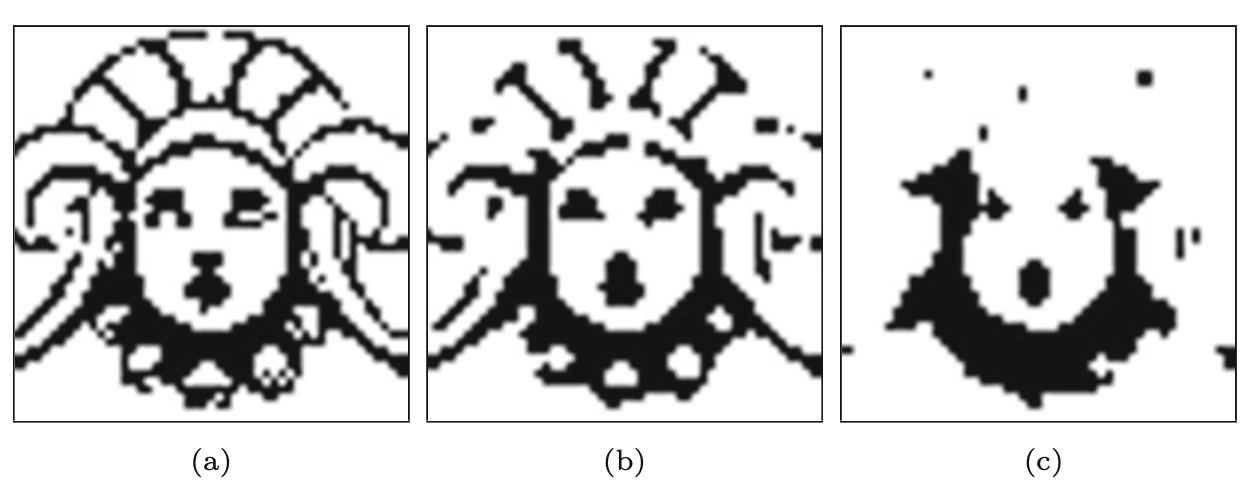
W swojej pierwotnej formie filtry morfologiczne były ukierunkowane na obrazy binarne, obrazy o tylko dwóch możliwych wartościach pikseli, odpowiednio 0 i 1 lub czarny i biały. Obrazy binarne spotykane są w wielu miejscach, w szczególności w druku cyfrowym, transmisji dokumentów (fax) i przechowywaniu danych, czy też jako maski selekcyjne w edycji obrazów i filmów. Obrazy binarne można uzyskać z obrazów w skali szarości poprzez proste progowanie z użyciem globalnej lub lokalnie zmiennej wartości progowej. Piksele binarne o wartościach 1 i 0 oznaczamy odpowiednio jako piksele pierwszego planu i tła. W większości poniższych przykładów piksele pierwszego planu są przedstawione w kolorze czarnym, a piksele tła w kolorze białym, tak jak to się dzieje w druku.
Pod koniec tego rozdziału przekonamy się, że filtry morfologiczne mają zastosowanie nie tylko do obrazów binarnych, ale także do obrazów w skali szarości, a nawet kolorowych, choć operacje te różnią się znacznie od ich binarnych odpowiedników.
Naszym punktem wyjścia była obserwacja, że prosty filtr medianowy o wymiarach 3×3 pikseli może zaokrąglić większe struktury obrazu i usunąć mniejsze, takie jak punkty i cienkie linie, w obrazie binarnym. Może to być przydatne do eliminacji struktur, które są poniżej pewnego rozmiaru (np. do oczyszczenia obrazu z szumów lub zanieczyszczeń). Ale jak możemy kontrolować rozmiar i ewentualnie kształt struktur dotkniętych taką operacją?
Chociaż jego efekty strukturalne mogą być interesujące, pomijamy w tym momencie filtr medianowy i zaczynamy to zadanie od początku. Załóżmy, że chcemy usunąć małe struktury z obrazu binarnego, nie zmieniając znacząco pozostałych większych struktur. Pomysł na realizacje tego zadania może być następujący:
- Najpierw wszystkie struktury w obrazie są iteracyjnie “zmniejszane” (lub “kurczenie”) przez odklejanie warstwy o określonej grubości wokół granic.
- Kurczenie usuwa krok po kroku mniejsze struktury i pozostają tylko większe.
- Pozostałe struktury są następnie powiększane o taką samą ilość.
- W końcu większe regiony powinny powrócić do mniej więcej swoich pierwotnych kształtów, podczas gdy mniejsze regiony zniknęły z obrazu.
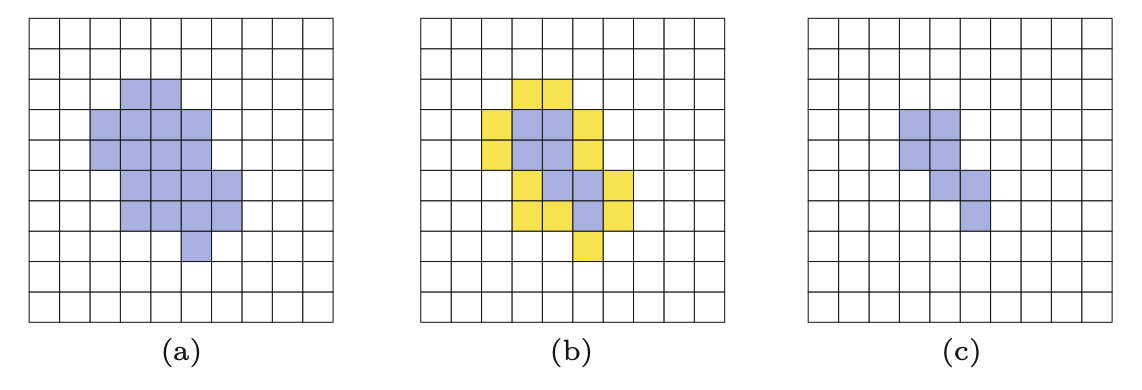
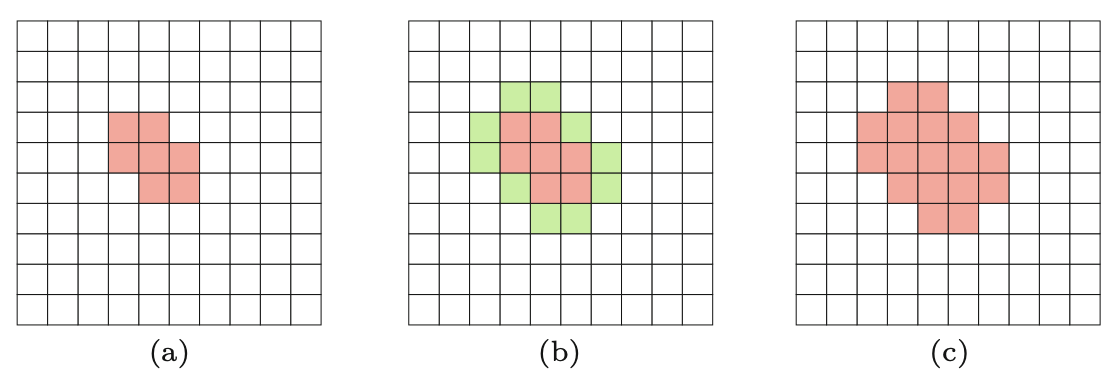
Potrzebujemy do tego jedynie dwóch rodzajów operacji. “Kurczenie” oznacza usunięcie warstwy pikseli z regionu pierwszoplanowego wokół wszystkich jego granic na tle (Rysunek 8.2). Z drugiej strony, “rośnięcie”, dodaje warstwę pikseli wokół granicy regionu pierwszoplanowego (Rysunek 8.3).
8.1 Identyfikacja sąsiadów
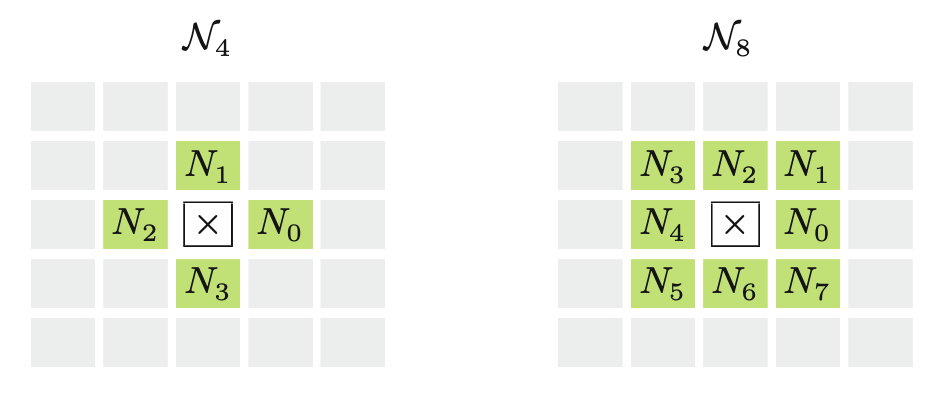
W przypadku prostokątnych siatek pikseli powszechnie stosowane są dwie definicje “sąsiedztwa”:
- cztery piksele sąsiadujące z danym pikselem w kierunku poziomym i pionowym;
- osiem sąsiadujących pikseli z analizowanym.
8.2 Podstawowe operacje morfologiczne
Zmniejszanie i zwiększanie to rzeczywiście dwie najbardziej podstawowe operacje morfologiczne, które są określane odpowiednio jako “erozja” (ang. erosion) i “dylatacja” (ang. dilation). Operacje te są jednak znacznie bardziej ogólne niż zilustrowane w przykładzie. Wykraczają one daleko poza usuwanie lub dołączanie warstw pojedynczych pikseli i - w połączeniu - mogą wykonywać znacznie bardziej złożone operacje.
8.2.1 Element strukturyzujący
Podobnie jak w przypadku macierzy współczynników filtru liniowego, właściwości filtru morfologicznego są określone przez elementy macierzy zwanej “elementem strukturyzującym”. W morfologii binarnej element strukturyzujący (podobnie jak sam obraz) zawiera tylko wartości 0, a “gorący punkt” (ang. hot spot) wyznacza początek układu współrzędnych \(H\) (Rysunek 8.5). Przy czym, hot spot nie musi znajdować się w środku elementu strukturyzującego, ani jego wartość nie musi być równa 1.

8.2.1.1 Zbiór punktowy
Dla formalnej specyfikacji operacji morfologicznych pomocne jest czasem opisanie obrazów binarnych jako zbiorów punktów o współrzędnych 2D. Dla obrazu binarnego \(I(u, v) \in \{0, 1\}\), odpowiadający zbiór punktów \(\mathcal{Q}_I\) składa się z par współrzędnych \(p = (u, v)\) wszystkich pikseli pierwszego planu,
\[ \mathcal{Q}_I =\{p\vert I(p)=1\}. \tag{8.1}\]
Oczywiście, jak pokazano na Rysunek 8.5, nie tylko obraz binarny \(I\), ale również element strukturyzujący \(H\) może być opisany jako zbiór punktów.

Dzięki temu, że opisujemy je jako zbiory punktów, podstawowe operacje na obrazach binarnych można również wyrazić jako proste operacje na zbiorach. Na przykład, odwrócenie obrazu binarnego \(I \rightarrow \bar{I}\) (czyli zamiana pierwszego planu i tła) jest równoważne zbudowaniu zbioru dopełniającego
\[ \mathcal{Q}_{\bar{I}}=\bar{\mathcal{Q}}_I=\{p\in \mathbb{Z}^2\vert p\notin \mathcal{Q}_I\}. \tag{8.2}\]
Łącząc dwa obrazy binarne \(I_1\) i \(I_2\) za pomocą operacji OR między odpowiadającymi im pikselami, otrzymany zbiór punktów jest unią indywidualnych zbiorów punktów \(Q_{I_1}\) i \(Q_{I_2}\). Ponieważ zbiór punktów \(Q_I\) jest tylko alternatywną reprezentacją obrazu binarnego \(I\) (tzn. \(I = Q_I\)), to w dalszej części będziemy używać synonimicznie obu notacji: obrazu i zbioru.
8.2.1.2 Dylatacja
Dylatacja jest operacją morfologiczną, która odpowiada naszemu intuicyjnemu pojęciu “wzrastania”, omówionemu już wcześniej. Jako operacja na zbiorach, jest ona zdefiniowana jako
\[ I\oplus H= \{(p+q)| p\in I, q\in H \}. \tag{8.3}\]
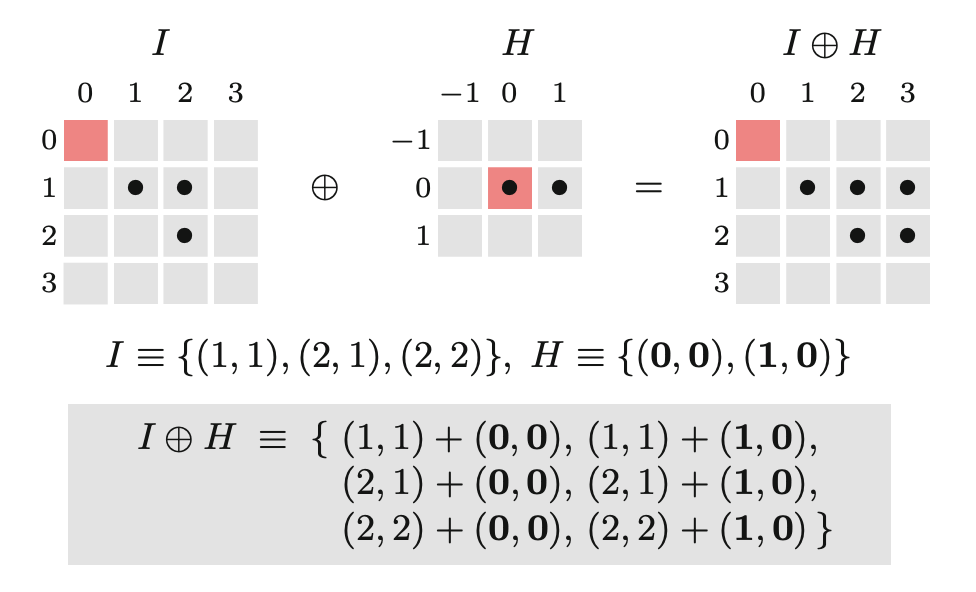
Tak więc zbiór punktów powstały w wyniku dylatacji jest sumą (wektorową) wszystkich możliwych par punktów współrzędnych z oryginalnych zbiorów \(I\) i \(H\), co ilustruje prosty przykład na Rysunek 8.7. Alternatywnie można postrzegać dylatację jako powielenie elementu struktury \(H\) na każdy piksel pierwszego planu obrazu \(I\) lub, odwrotnie, powielenie obrazu \(I\) na każdy element pierwszego planu \(H\).
8.2.1.3 Erozja
Quasi-odwrotnością dylatacji jest operacja erozji, ponownie zdefiniowana w notacji zbiorów jako
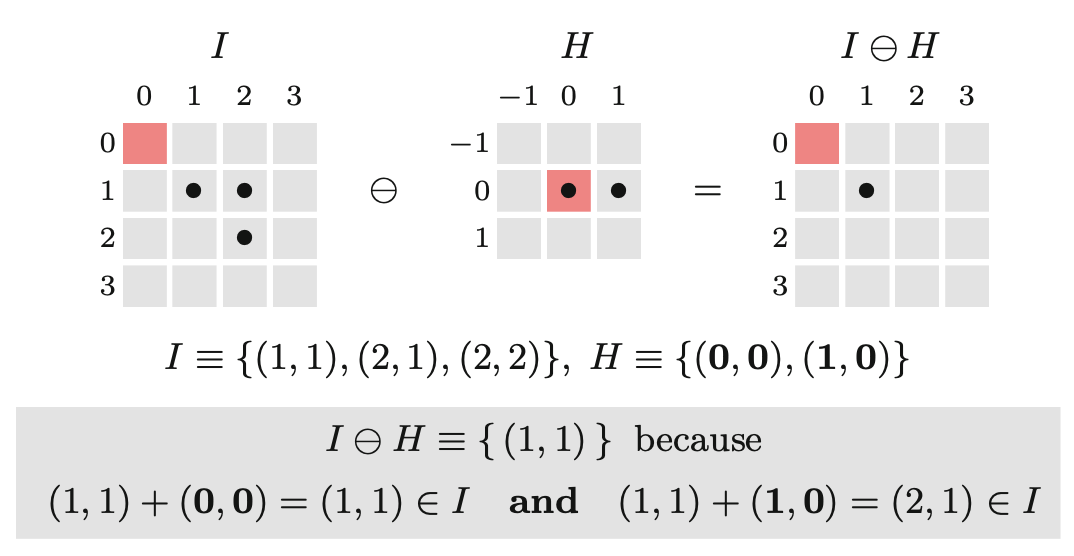
\[ I\ominus H= \{p\in \mathbb{Z}^2| (p+q)\in I, q\in H \}. \tag{8.4}\]
Operację tę można zinterpretować następująco. Pozycja \(p\) jest zawarta w wyniku \(I \ominus H\) wtedy (i tylko wtedy), gdy element strukturyzujący \(H\) - po umieszczeniu w tej pozycji \(p\) - jest w całości zawarty w pikselach pierwszego planu oryginalnego obrazu. Rysunek 8.8 przedstawia przykład erozji.
Filtr morfologiczny jest jednoznacznie określony przez (a) rodzaj operacji i (b) zawartość elementu strukturyzującego. Odpowiedni rozmiar i kształt elementu strukturyzującego zależy od zastosowania, rozdzielczości obrazu itp. W praktyce często stosuje się elementy strukturyzujące o quasi-kolistym kształcie.

Dylatacja z wykorzystaniem okrągłego (dyskowego) elementu strukturyzującego o promieniu \(r\) powoduje dodanie warstwy o szerokości \(r\) do każdej struktury pierwszoplanowej w obrazie. I odwrotnie, erozja z tym elementem strukturyzującym usuwa warstwy o tej samej szerokości. Na Rysunek 8.9 przedstawiono wyniki dylatacji i erozji z użyciem dyskowych elementów strukturyzujących o różnych średnicach, zastosowanych do oryginalnego obrazu z rysunku.
Wyniki dylatacji i erozji dla różnych innych elementów strukturyzujących pokazano na Rysunek 8.10.

8.2.1.4 Otwarcie i zamknięcie
Złożenia funkcji dylatacji i erozji w odpowiedniej kolejności tworzą nowe transformacje nazywane otwarciem (ang. opening) i zamknięciem (ang. closing). Są one prawdopodobnie najczęściej używanymi przekształceniami morfologicznymi.
Otwarcie binarne \(I\circ H\) oznacza erozję, po której następuje dylatacja z tym samym elementem strukturyzującym \(H\), czyli
\[ I\circ H=(I\ominus H)\oplus H. \tag{8.5}\]
Głównym efektem otwarcia jest to, że wszystkie struktury pierwszego planu, które są mniejsze niż element strukturyzujący, są eliminowane w pierwszym kroku (erozja). Pozostałe struktury są wygładzane przez dylatację i powiększane w przybliżeniu do ich pierwotnego rozmiaru, jak pokazano na przykładach na Rysunek 8.11. Ten proces kurczenia się, a następnie wzrostu odpowiada idei eliminacji małych struktur, którą wstępnie naszkicowaliśmy wcześniej.
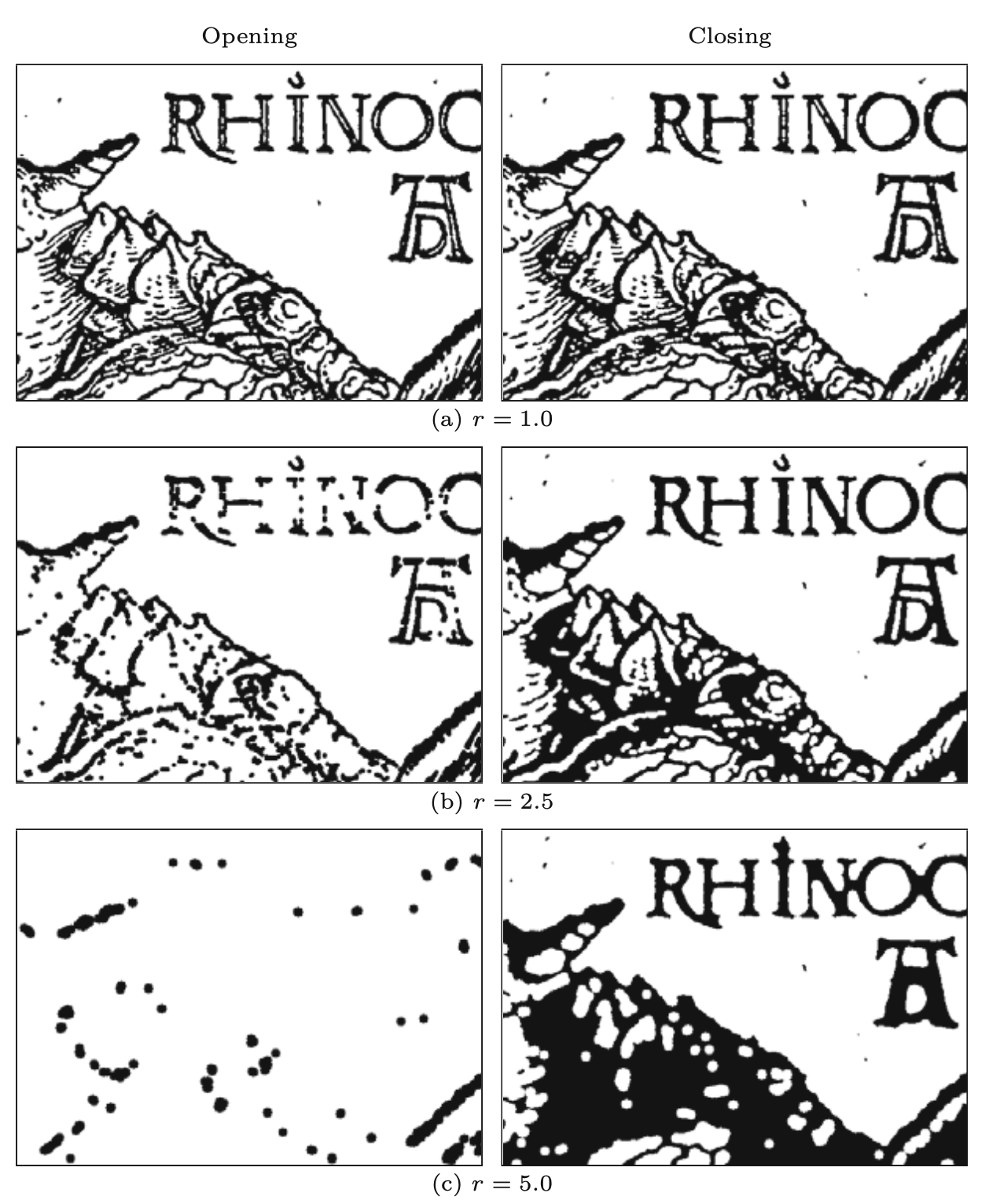
Gdy odwrócimy kolejność erozji i dylatacji, otrzymaną operację nazywamy domknięciem i oznaczamy \(I\bullet H\)
\[ I\bullet H=(I\oplus H)\ominus H. \tag{8.6}\]
Zamknięcie usuwa (zamyka) otwory i szczeliny w strukturach pierwszego planu, które są mniejsze niż element strukturyzujący \(H\). Kilka przykładów z typowymi elementami strukturyzującymi w kształcie dysku pokazano na Rysunek 8.11.
8.2.1.5 Przerzedzanie
Przerzedzanie lub rozrzedzanie (ang. thininng) zwane też szkieletyzacją (ang. skeletonization) jest powszechną techniką morfologiczną, której celem jest zmniejszenie struktur binarnych do maksymalnej szerokości jednego piksela bez dzielenia ich na wiele części. Osiąga się to poprzez iteracyjną erozję “warunkową”. Jest ona stosowana w lokalnym sąsiedztwie tylko wtedy, gdy pozostaje wystarczająco szeroka struktura i operacja nie powoduje separacji. Wymaga to, aby w zależności od lokalnej struktury obrazu, w każdej pozycji obrazu podejmowana była decyzja, czy można zastosować kolejny krok erozji, czy też nie. Operacja jest kontynuowana do momentu, gdy w obrazie wynikowym nie pojawią się już żadne zmiany. Wynika z tego, że w porównaniu ze zwykłą (“homogeniczną”) morfologią omówioną wcześniej, thinning jest kosztowny obliczeniowo. Częstym zastosowaniem rozrzedzania jest obliczanie “szkieletu” regionu binarnego, np. w celu strukturalnego dopasowania kształtów 2D.
Rozrzedzanie znane jest również pod terminami wykrywanie linii środkowej i transformacji osi środkowej. Istnieje wiele różnych implementacji o zróżnicowanej złożoności i wydajności. Poniżej opisujemy klasyczny algorytm autorstwa Zhang i Suen (1984) oraz jego implementację jako reprezentatywny przykład.
Wejściem do tego algorytmu jest obraz binarny \(I\), w którym piksele pierwszego planu mają wartość 1, a piksele tła wartość 0. Algorytm skanuje obraz i w każdej pozycji \((u, v)\) bada sąsiedztwo rozmiaru 3x3 z centralnym elementem \(P\) i otaczającymi go wartościami \(N = (N_0, N_1, \ldots , N_7)\).
W celu sklasyfikowania zawartości lokalnego sąsiedztwa \(N\) definiujemy najpierw funkcję
\[ B(N)=N_0+N_1+\dots+N_7=\sum_{i=0}^7N_i, \tag{8.7}\]
która zlicza piksele otaczającego tła. Definiujemy również tzw. liczbę połączeń, która wyraża ile składowych binarnych jest połączonych poprzez bieżący piksel centralny w pozycji \((u, v)\). Wielkość ta jest równoważna liczbie przejść \(1\to 0\) w ciągu \((N_0, . . . , N_7, N_0)\), lub wyrażona w sposób arytmetyczny
\[ C(N)=\sum_{i=0}^7N_i\cdot [N_i-N_{(i+1) \text{ mod }8}]. \tag{8.8}\]
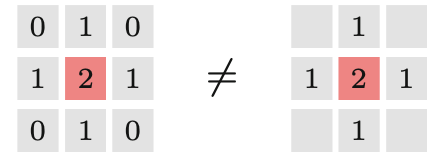
Rysunek 8.12 przedstawia kilka wybranych przykładów dla sąsiedztwa \(N\) oraz związane z nimi wartości funkcji \(B(N)\) i \(C(N)\). Na podstawie powyższych funkcji definiujemy ostatecznie dwa predykaty boolowskie \(R_1,R_2\) na sąsiedztwie \(N\).
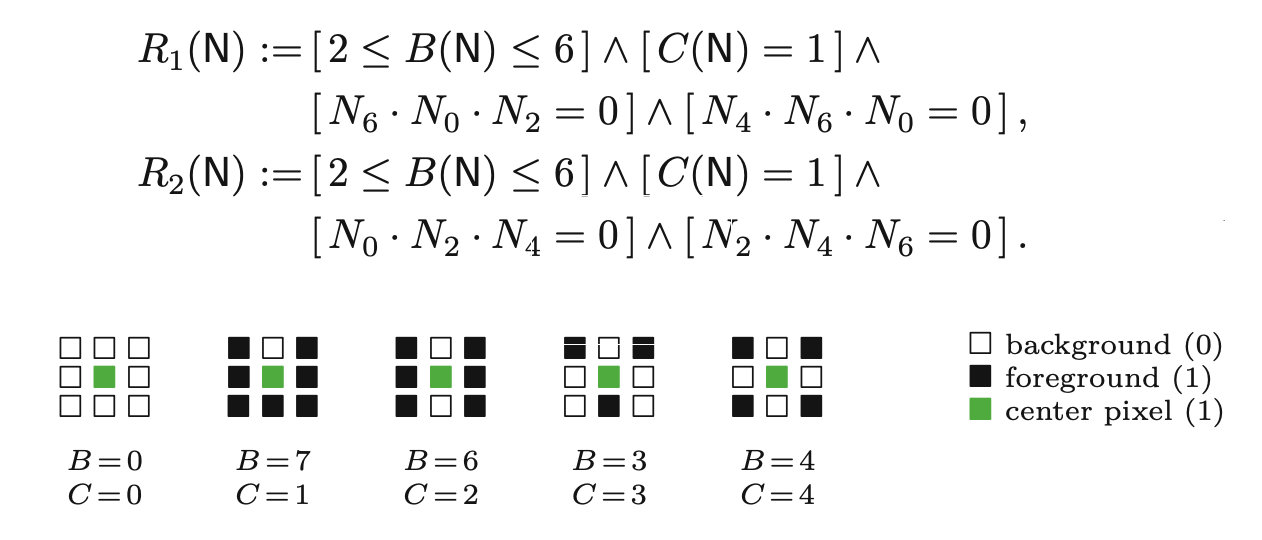
W zależności od wyniku \(R_1(N)\) i \(R_2(N)\) piksel pierwszego planu na środkowej pozycji \(P\) jest albo usuwany (czyli erodowany), albo oznaczany jako nieusuwalny.
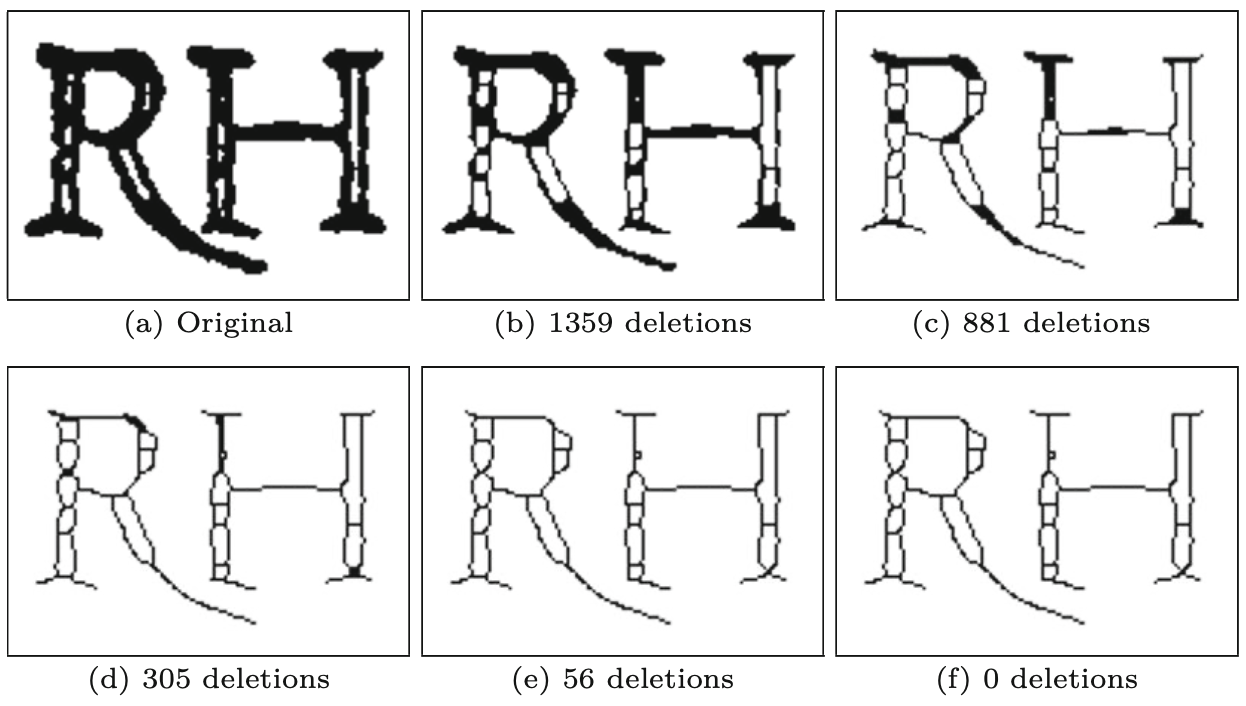
Rysunek 8.13 ilustruje efekt rozrzedzania warstwa po warstwie wykonywanego przez kolejne iteracje tej procedury. W każdej iteracji selektywnie usuwana jest tylko jedna “warstwa” pikseli pierwszego planu.
8.3 Operacje morfologiczne w skali szarości i na obrazach kolorowych
Operacje morfologiczne nie ograniczają się do obrazów binarnych, ale dotyczą również obrazów intensywnościowych (w skali szarości). W rzeczywistości, definicja morfologii skali szarości jest uogólnieniem morfologii binarnej, przy czym binarne operatory OR i AND zostały zastąpione przez arytmetyczne operatory MAX i MIN, odpowiednio. W konsekwencji procedury przeznaczone do morfologii w skali szarości mogą również wykonywać morfologię binarną (ale nie odwrotnie). W przypadku obrazów kolorowych, operacje w skali szarości są zwykle stosowane indywidualnie do każdego kanału kolorystycznego.
8.3.1 Element strukturyzujący
Inaczej niż w schemacie binarnym, elementy strukturyzujące dla morfologii w skali szarości nie są zdefiniowane jako zbiory punktów, lecz jako funkcje rzeczywiste 2D, czyli
\[ H(i,j)\in\mathbb{R}, \quad (i,j)\in\mathbb{Z}^2. \tag{8.9}\]
Wartości w \(H\) mogą być ujemne lub zerowe. Zauważmy jednak, że w przeciwieństwie do konwolucji liniowej, elementy zerowe w morfologii skali szarości mają na ogół swój udział w wyniku. Element strukturyzujący dla morfologii w skali szarości musi zatem wyraźnie rozróżniać komórki zawierające wartość 0 i komórki puste, na przykład
8.3.1.1 Dylatacja i erozja
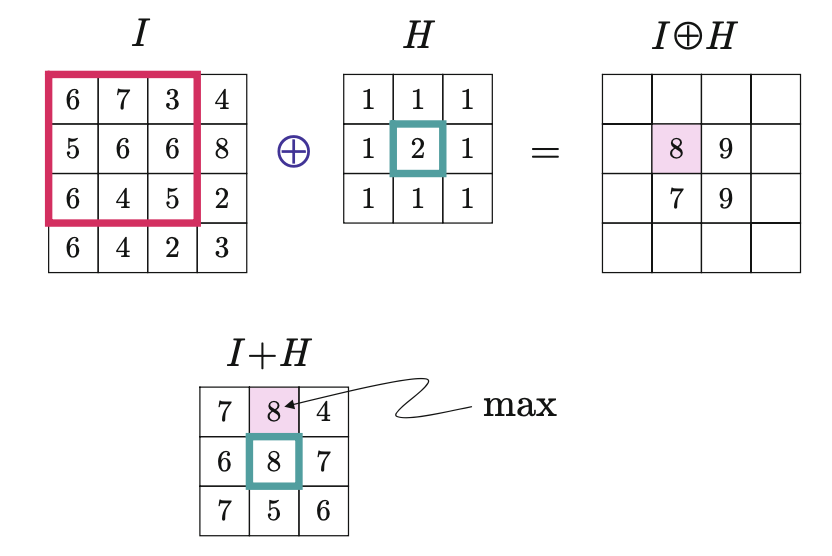
Wynik dylatacji w skali szarości \(I\oplus H\) definiujemy jako maksimum wartości w \(H\) dodane do wartości bieżącego podobrazu \(I\), czyli
\[ (I\oplus H)(u,v)=\max_{(i,j)\in H}(I(u+i,v+j)+H(i,j)). \tag{8.10}\]
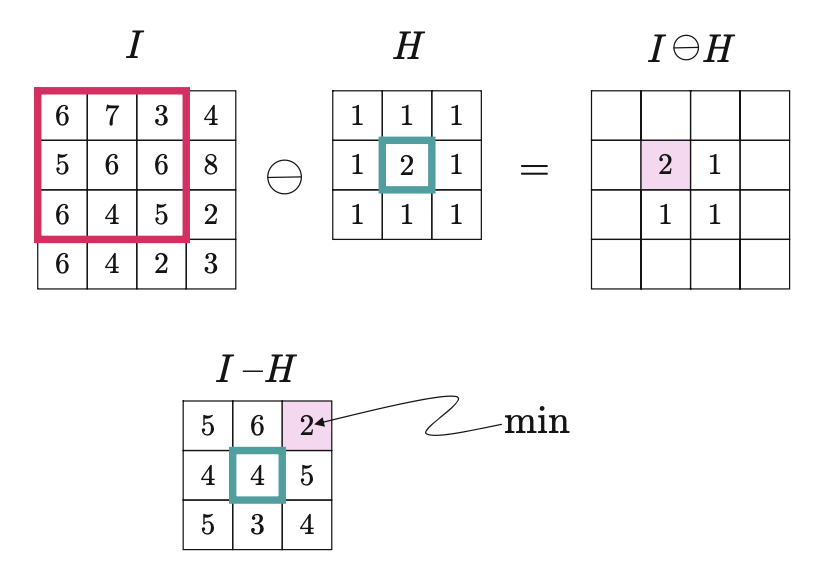
Podobnie wynik erozji w skali szarości to minimum różnic
\[ (I\ominus H)(u,v)=\max_{(i,j)\in H}(I(u+i,v+j)-H(i,j)). \tag{8.11}\]
Na Rysunek 8.14 i Rysunek 8.15 zademonstrowano na prostym przykładzie podstawowy proces, odpowiednio, dylatacji i erozji w skali szarości.
8.3.1.2 Otwarcie i domknięcie
Otwarcie i domknięcie na obrazach w skali szarości definiuje się, identycznie jak w przypadku binarnym, jako operacje złożone z dylatacji i erozji z tym samym elementem strukturyzującym. Kilka przykładów pokazano na Rysunek 8.16 dla elementów strukturyzujących w kształcie dysku oraz na Rysunek 8.17 dla różnych niestandardowych elementów strukturyzujących. Zauważ, że można uzyskać interesujące efekty, szczególnie w przypadku elementów strukturyzujących przypominających kształtem pędzel lub inne wzory pociągnięć.


