9 Optymalizacja modeli
Część modeli, jak np. regresja liniowa, posiada wszystkie parametry, które da się oszacować na podstawie zbioru uczącego. Są też modele, których parametry (przynajmniej część z nich) nie da się oszacować na podstawie próby. Przykładem może być model kNN, w którym \(k\) jest parametrem, którego wartość nie jest estymowana w czasie uczenia modelu. Takich przykładów można mnożyć, przykładowo głębokość drzew czy minimalna wielkość węzła aby dokonać podziału w lesie losowym również są parametremi, których wartości nie da się szacować w procesie uczenia modelu. Takie “odmienne” parametry będziemy nazywać hiperparametrami modelu.
Czy to oznacza, że jesteśmy zdani na ich zgadywanie? 🙈 Na szczęście nie. Proces w którym odbywa się poszukiwanie optymalnych parametrów modelu nazywamy optymalizacją modelu (ang. tuning). Definicję tę można nawet rozszerzyć, jeśli pomyślimy o dostosowaniu takich parametrów jak szybkość uczenia sieci neuronowej, rodzaj metody gradientowej, czy liczba iteracji/epok w procesie uczenia. Co więcej również w procesie przygotowania danych do modelowania, występują parametry, których wartość należy optymalizować. Przykładowo liczba składowych głównych w PCA jest hiperparametrem, którego wartość należy dostrajać. Nawet w kontekście wspomnianych klasycznych modeli jak np. regresja możemy optymalizować model pod kątem wyboru funkcji łączącej.
Jak zatem przeprowadzić optymalizację modelu, skoro tak wiele różnych parametrów może wpłynąć na ostateczną jego postać? To zależy od tego co chcemy optymalizować. Przykładowo jeśli obiektem naszych zainteresowań jest wybór najlepszej funkcji łączącej, to powinniśmy użyć do tego funkcji celu jako miary oceniającej rozwiązania. Friedman (2001) pokazał, że optymalna liczba drzew będzie inna jeśli w procesie optymalizacji użyjemy dwóch różnych kryteriów oceny modelu - funkcji wiarogodności i dokładności (accuracy).
Kod
set.seed(44)
split <- initial_split(two_class_dat, prop = 0.8)
training_set <- training(split)
testing_set <- testing(split)
llhood <- function(...) {
logistic_reg() %>%
set_engine("glm", ...) %>%
fit(Class ~ ., data = training_set) %>%
glance() %>%
select(logLik)
}
bind_rows(
llhood(),
llhood(family = binomial(link = "probit")),
llhood(family = binomial(link = "cloglog"))
) %>%
mutate(link = c("logit", "probit", "c-log-log")) %>%
arrange(desc(logLik))# A tibble: 3 × 2
logLik link
<dbl> <chr>
1 -270. logit
2 -274. probit
3 -286. c-log-logBiorąc pod uwagę powyższe wyniki model logistyczny okazuje się być najlepszy. Porównanie to niestety wyrażone zostało pojedynczą statystyką dla każdego modelu. Zatem nie możemy stwierdzić, czy różnice te są istotne statystycznie. Aby tego dokonać porównamy funkcje straty na podstawie resamplingu.
Kod
set.seed(1201)
rs <- vfold_cv(training_set, repeats = 10)
# Return the individual resampled performance estimates:
lloss <- function(...) {
perf_meas <- metric_set(roc_auc, mn_log_loss)
logistic_reg() %>%
set_engine("glm", ...) %>%
fit_resamples(Class ~ A + B, rs, metrics = perf_meas) %>%
collect_metrics(summarize = FALSE) %>%
select(id, id2, .metric, .estimate)
}
resampled_res <-
bind_rows(
lloss() %>% mutate(model = "logistic"),
lloss(family = binomial(link = "probit")) %>% mutate(model = "probit"),
lloss(family = binomial(link = "cloglog")) %>% mutate(model = "c-log-log")
) %>%
# Convert log-loss to log-likelihood:
mutate(.estimate = ifelse(.metric == "mn_log_loss", -.estimate, .estimate)) %>%
group_by(model, .metric) %>%
summarize(
mean = mean(.estimate, na.rm = TRUE),
std_err = sd(.estimate, na.rm = TRUE) / sum(!is.na(.estimate)),
.groups = "drop"
)
resampled_res %>%
filter(.metric == "mn_log_loss") %>%
ggplot(aes(x = mean, y = model)) +
geom_point() +
geom_errorbar(aes(xmin = mean - 1.96 * std_err, xmax = mean + 1.96 * std_err),
width = .1) +
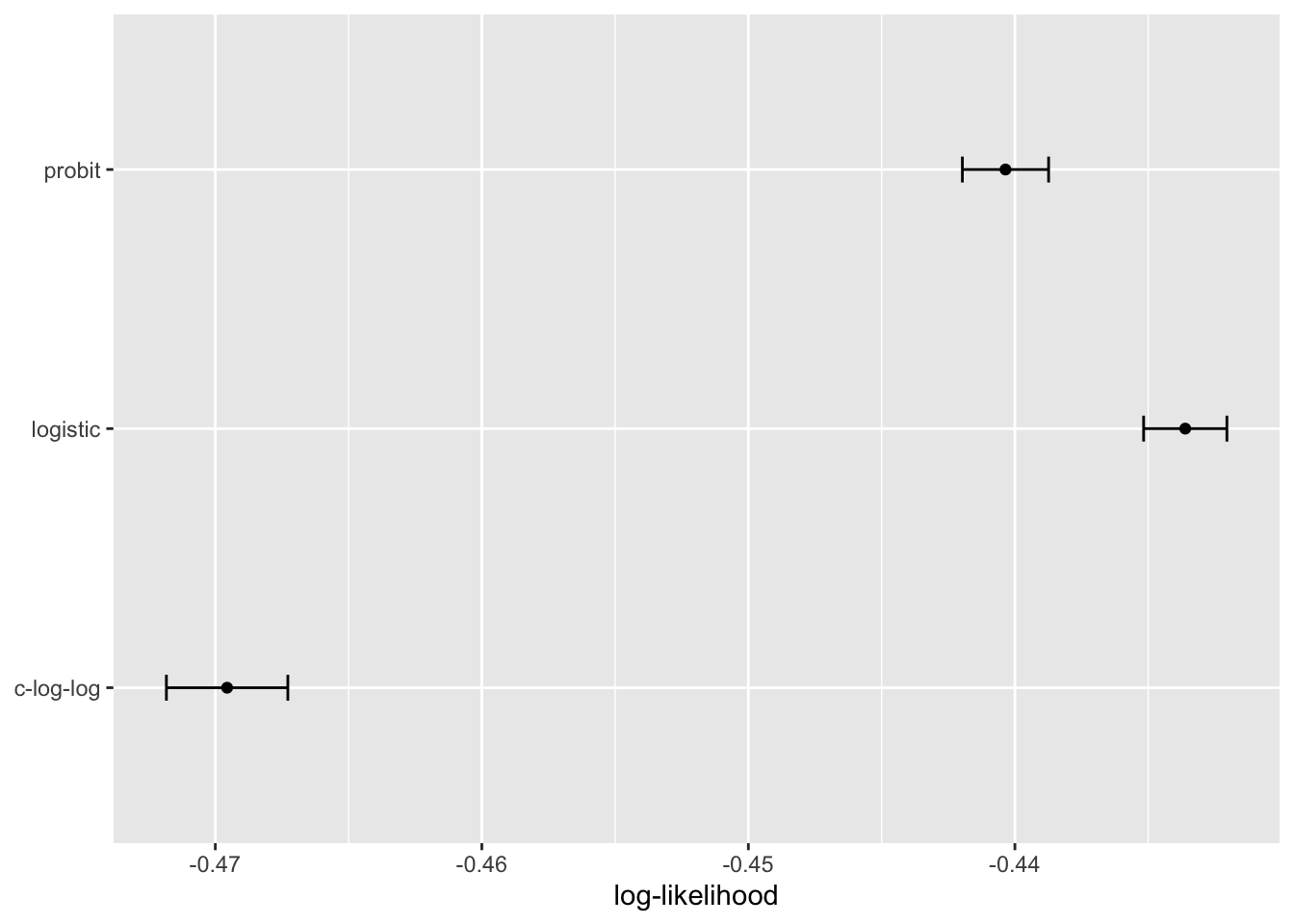
labs(y = NULL, x = "log-likelihood")Skala tych wartości jest inna niż poprzednich, ponieważ są one obliczane na mniejszym zbiorze danych; wartość uzyskana przez broom::glance() jest sumą, podczas gdy yardstick::mn_log_loss() jest średnią. Wyniki te pokazują, że istnieją znaczne dowody na to, że wybór funkcji łączącej ma znaczenie i że model logistyczny jest lepszy.
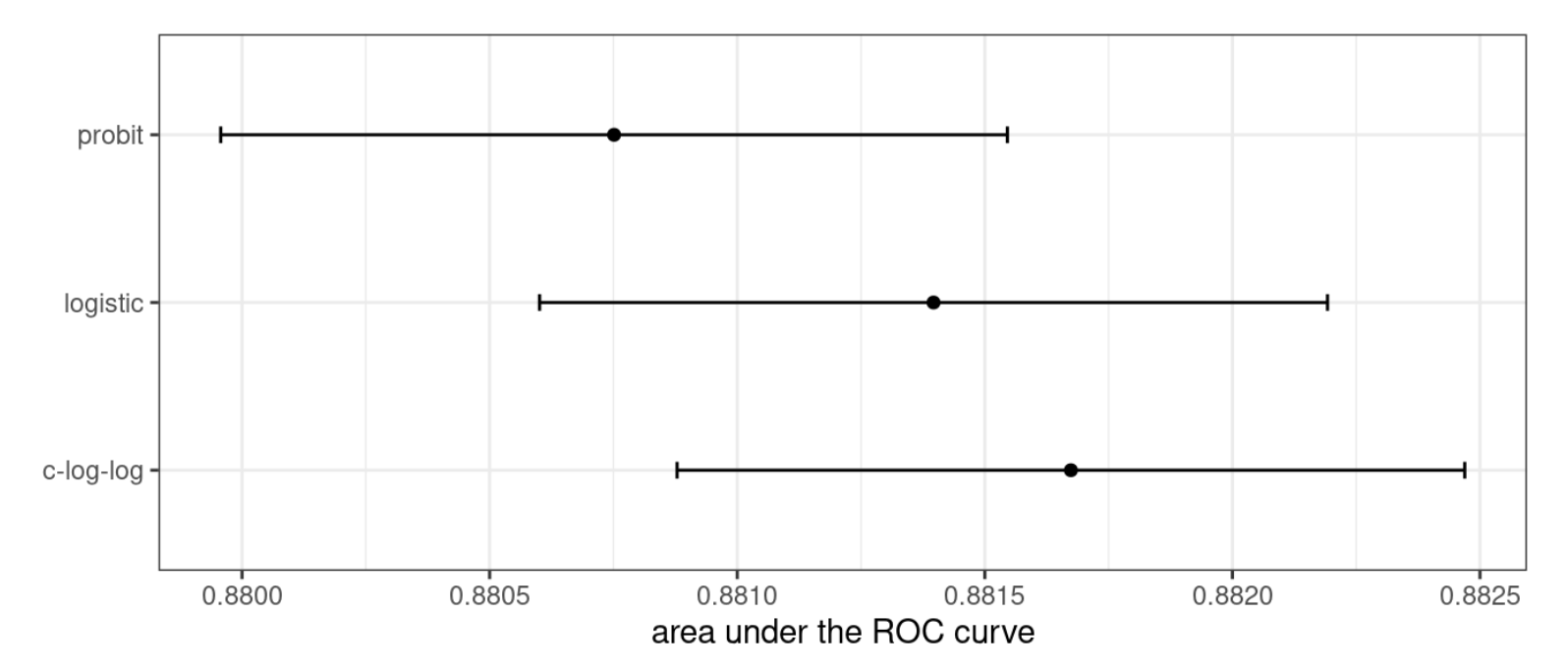
A co gdy użyjemy innej miary oceny dopasowania?
Jak widać zastosowanie innej miary powoduje, po pierwsze zmianę kolejności (najlepszy okazał się model c-log-log), a po drugie różnice pomiędzy modelami się zatarły.
To ćwiczenie pokazuje, że różne metryki mogą prowadzić do różnych decyzji dotyczących wyboru wartości parametrów. W tym przypadku jedna metryka wydaje się wyraźnie sortować modele, podczas gdy inna nie wykazuje żadnej różnicy.
Thomas i Uminsky (2020) sugeruje, że aby uniknąć pewnego rodzaju dwuznaczności oraz “gry” metrykami1 należy używać całych zestawów metryk, które dadzą pełniejszy obraz oraz konsultowania wyników z odbiorcami.
1 to jego oryginalne określenie mające ukazać problem doboru jednej metryki, wg której najlepszy model osiąga wysoką jakość dopasowania
9.1 Konsekwencje złego oszacowania parametrów
Wiele parametrów dostrajania modyfikuje stopień złożoności modelu. Większa złożoność często oznacza większą plastyczność wzorców, które model może naśladować. Na przykład, dodanie stopni swobody w funkcji splajnu zwiększa złożoność predykcji. Choć jest to zaleta, gdy motywacją są leżące u podstaw danych złożone zależności, może to również prowadzić do nadinterpretacji przypadkowych wzorców, które nie powtarzałyby się w nowych danych. Overfitting to sytuacja, w której model zbytnio dostosowuje się do danych treningowych; działa dobrze dla danych użytych do budowy modelu, ale słabo dla nowych danych.
Przyjrzyjmy się przykładowo modelowi jednowarstwowej sieci neuronowej z jedną warstwą wejściową i jedną warstwą ukrytą z sigmoidalną funkcjach aktywacji. Taka sieć neuronowa to, na dobrą sprawę, po prostu regresja logistyczna2. Jednak wraz ze wzrostem liczby neuronów w warstwie ukrytej rośnie złożoność modelu.
2 oczywiście tylko wtedy gdy warstwa ukryta ma jeden neuron, a wejściem do niego jest warstwa z aktywacją liniową
Dopasowaliśmy modele klasyfikacyjne sieci neuronowych do tych samych dwuklasowych danych z poprzedniego przykładu, zmieniając liczbę neuronów w warstwie ukrytej. Używając obszaru pod krzywą ROC jako metryki wydajności, skuteczność modelu na zbiorze treningowym rośnie wraz z dodawaniem kolejnych jednostek ukrytych. Model sieci dokładnie i skrupulatnie uczy się zbioru treningowego. Jeśli ocena modelu jest dokonywana na podstawie wartości ROC zbioru treningowego, to preferuje się wiele neuronów w warstwie ukrytej, tak aby można było prawie całkowicie wyeliminować błędy.
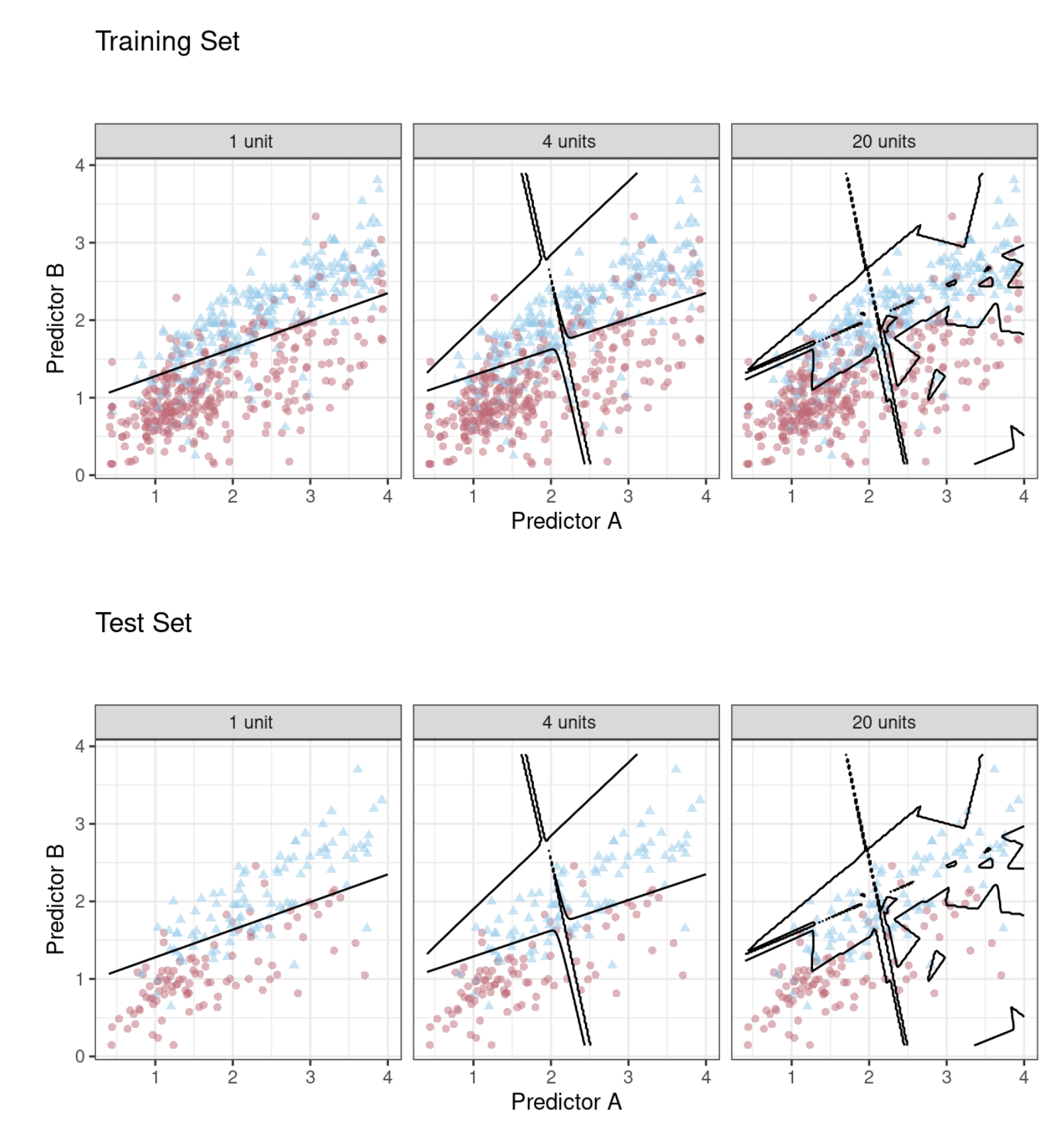
Rozdziały wcześniejsze pokazały, że ocena dopasowania na zbiorze uczącym jest złym podejściem do oceny modelu. W tym przypadku sieć neuronowa bardzo szybko zaczyna nadinterpretować wzorce, które widzi w zbiorze treningowym. Porównaj trzy przykładowe granice klas (opracowane na podstawie zbioru treningowego) nałożone na zbiory treningowe i testowe na Rys. 9.3.
Model z pojedynczym neuronem w warstwie ukrytej nie dostosowuje się zbyt elastycznie do danych (ponieważ jest ograniczony do bycia liniowym). Model z czterema jednostkami ukrytymi zaczyna wykazywać oznaki przeuczenia z nierealistyczną granicą dla wartości oddalonych od chmury danych. Dla 20 neuronów ukrytych model zaczyna zapamiętywać zbiór treningowy, tworząc małe wyspy wokół pojedynczych obserwacji, aby zminimalizować współczynnik błędu. Wzorce te nie powtarzają się w zbiorze testowym. W przypadku modelu składającego się z 20 jednostek, współczynnik ROC AUC dla zbioru treningowego wynosi 0,944, ale wartość dla zbioru testowego to 0,855.
9.2 Dwa podejścia do tuningu
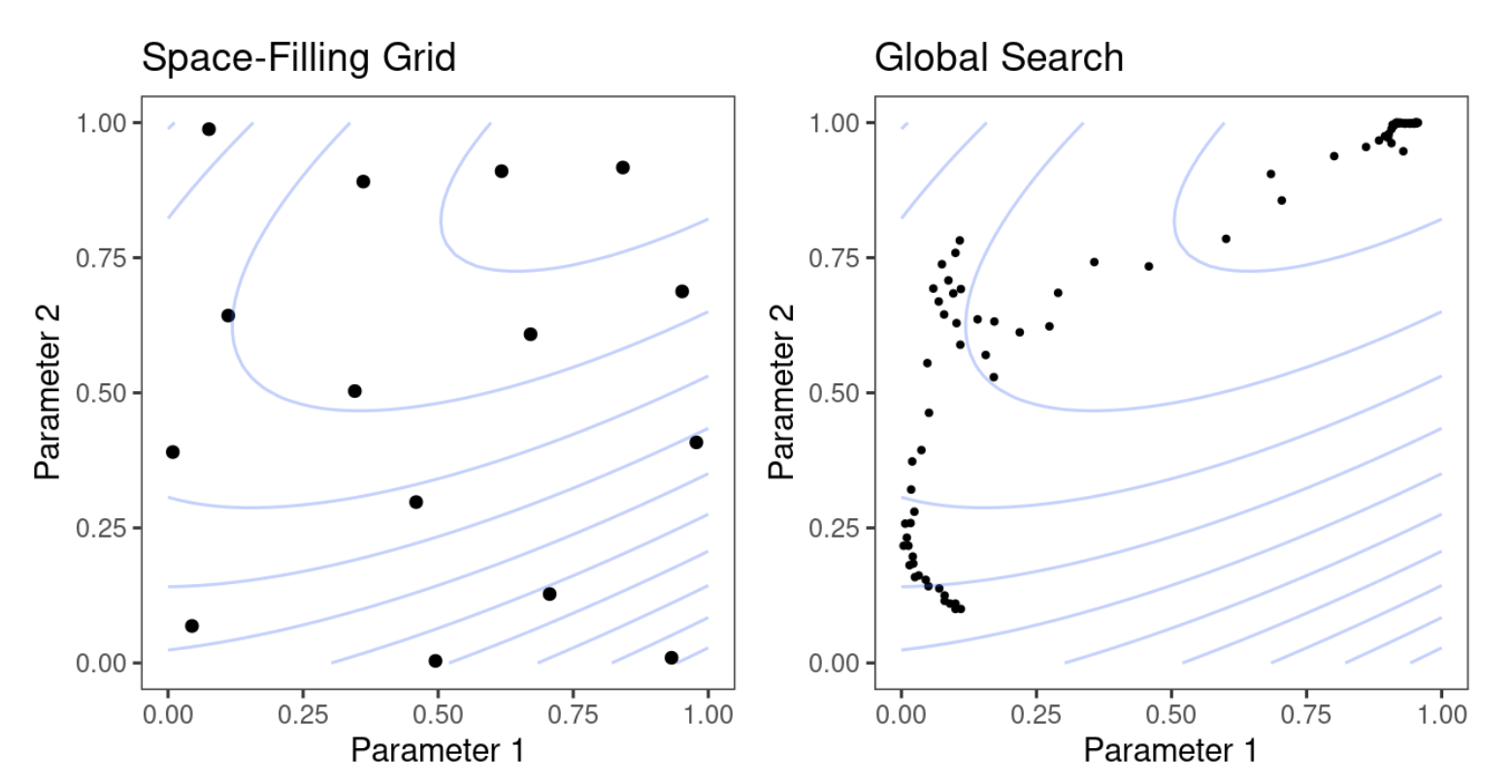
Istnieją dwa sposoby realizacji tuningu modeli:
- przeszukiwanie siatki - gdy wstępnie określamy zestaw wartości parametrów do oceny. Głównymi problemami związanymi z przeszukiwaniem siatki są sposób wykonania siatki i liczba kombinacji parametrów do oceny. Przeszukiwanie siatki jest często oceniane jako nieefektywne, ponieważ liczba punktów siatki wymaganych do pokrycia przestrzeni parametrów może stać się niemożliwa do opanowania. Z jednej strony ten fakt przemawiałby za nie wybieraniem tej metody do poszukiwania optymalnych parametrów, ale jest to najbardziej uzasadniona metoda, gdy proces nie jest zoptymalizowany w kontekście kierunków przeszukiwania.
- przeszukiwanie iteracyjne lub sekwencyjne - gdy sekwencyjnie odkrywamy nowe kombinacje parametrów na podstawie poprzednich wyników. W niektórych przypadkach do rozpoczęcia procesu optymalizacji wymagany jest wstępny zestaw wyników dla jednej lub więcej kombinacji parametrów.
Można też stosować rozwiązania hybrydowe, gdzie metoda siatki jest stosowana do wstępnego oszacowania parametrów modelu, a następnie metodami iteracyjnymi korygowane są wspomniane parametry.
W procesie dostrajania modelu, możemy szacować hiperparametry główne oraz specyficzne dla danego silnika metody.
Kod
rand_forest(trees = 2000, min_n = 10) %>% # <- main arguments
set_engine("ranger", regularization.factor = 0.5) # <- engine-specificAby przekazać informację do przebiegu pracy, że chcemy kalibrować pewne parametry modelu, należy podstawić pod ich wartości funkcję tune().
Kod
neural_net_spec <-
mlp(hidden_units = tune()) %>%
set_mode("regression") %>%
set_engine("keras")Chcąc zobaczyć jak model interpretuje takie podstawienie możemy użyć
Kod
extract_parameter_set_dials(neural_net_spec)Wyniki pokazują wartość nparam[+], co wskazuje, że liczba jednostek ukrytych jest parametrem liczbowym. Istnieje opcjonalny argument identyfikacyjny, który kojarzy nazwę z parametrami. Może się to przydać, gdy ten sam rodzaj parametrów jest dostrajany w różnych miejscach. Na przykład, w przypadku danych dotyczących mieszkania w Ames, przepis zakodował zarówno długość jak i szerokość geograficzną za pomocą funkcji spline. Jeśli chcemy dostroić dwie funkcje splajnu, aby potencjalnie miały różne poziomy gładkości, wywołujemy step_ns() dwukrotnie, raz dla każdego predyktora. Aby parametry były identyfikowalne, argument “identyfikator” może przyjąć dowolny ciąg znaków:
Kod
set.seed(1001)
ames <- ames |>mutate(Sale_Price = log10(Sale_Price))
ames_split <- initial_split(ames, prop = 0.80, strata = Sale_Price)
ames_train <- training(ames_split)
ames_test <- testing(ames_split)
ames_rec <-
recipe(Sale_Price ~ Neighborhood + Gr_Liv_Area + Year_Built + Bldg_Type +
Latitude + Longitude, data = ames_train) %>%
step_log(Gr_Liv_Area, base = 10) %>%
step_other(Neighborhood, threshold = tune()) %>%
step_dummy(all_nominal_predictors()) %>%
step_interact( ~ Gr_Liv_Area:starts_with("Bldg_Type_") ) %>%
step_ns(Longitude, deg_free = tune("longitude df")) %>%
step_ns(Latitude, deg_free = tune("latitude df"))
recipes_param <- extract_parameter_set_dials(ames_rec)
recipes_paramGdy receptura i specyfikacja modelu są połączone za pomocą przepływu pracy, oba zestawy parametrów są wyświetlane.
Kod
wflow_param <-
workflow() %>%
add_recipe(ames_rec) %>%
add_model(neural_net_spec) %>%
extract_parameter_set_dials()
wflow_paramW tym przypadku dodanie splajnów do sieci neuronowej jest tylko na potrzeby przykładu, ponieważ sama sieć neuronowa jest w stanie zamodelować dowolnie złożone zależności (w tym splajny) 🙉.
Każdy argument parametru dostrajania ma odpowiadającą mu funkcję w pakiecie dials. W zdecydowanej większości przypadków funkcja ma taką samą nazwę jak argument parametru:
Kod
hidden_units()
threshold()Parametr deg_free jest kontrprzykładem - pojęcie stopni swobody pojawia się w wielu różnych kontekstach. Gdy używamy splajnów, istnieje wyspecjalizowana funkcja dials o nazwie spline_degree(), która jest domyślnie wywoływana dla splajnów:
Kod
spline_degree()Pakiet dials posiada również funkcję wygodną do wyodrębnienia konkretnego obiektu parametru:
Kod
wflow_param %>% extract_parameter_dials("threshold")Wewnątrz zestawu parametrów, zakres parametrów może być również aktualizowany:
W niektórych przypadkach łatwo jest mieć rozsądne wartości domyślne dla zakresu możliwych wartości. W innych przypadkach zakres parametrów jest zależny od zbioru danych i nie można go założyć. Podstawowym parametrem dostrajania parametrów dla modeli lasu losowego jest liczba kolumn predyktorów, które są losowo próbkowane dla każdego podziału drzewa, zwykle oznaczana jako mtry(). Bez znajomości liczby predyktorów, ten zakres parametrów nie może być wstępnie skonfigurowany i wymaga finalizacji.
Kod
rf_spec <-
rand_forest(mtry = tune()) %>%
set_engine("ranger", regularization.factor = tune("regularization")) %>%
set_mode("regression")
rf_param <- extract_parameter_set_dials(rf_spec)
rf_paramKompletne obiekty parametrów mają [+] w podsumowaniu; wartość [?] wskazuje, że brakuje przynajmniej jednego końca możliwego zakresu. Istnieją dwie metody radzenia sobie z tym problemem. Pierwszą jest użycie update(), aby dodać zakres na podstawie tego, co wiesz o wymiarach danych:
Jednak to podejście może nie działać, jeśli receptura jest dołączona do przepływu pracy, który używa kroków dodających lub odejmujących kolumny. Jeśli te kroki nie są przeznaczone do dostrajania, funkcja finalize() może wykonać recepturę raz, aby uzyskać wymiary:
Kod
pca_rec <-
recipe(Sale_Price ~ ., data = ames_train) %>%
# Select the square-footage predictors and extract their PCA components:
step_normalize(contains("SF")) %>%
# Select the number of components needed to capture 95% of
# the variance in the predictors.
step_pca(contains("SF"), threshold = .95)
updated_param <-
workflow() %>%
add_model(rf_spec) %>%
add_recipe(pca_rec) %>%
extract_parameter_set_dials() %>%
finalize(ames_train)
updated_param
updated_param %>% extract_parameter_dials("mtry")Gdy receptura jest przygotowana, funkcja finalize() uczy się ustawiać górny zakres mtry na 74 predyktory. Dodatkowo, wyniki extract_parameter_set_dials() będą zawierały parametry specyficzne dla silnika (jeśli takie istnieją). Są one odkrywane w taki sam sposób jak główne argumenty i włączane do zestawu parametrów. Pakiet dials zawiera funkcje parametrów dla wszystkich potencjalnie przestrajalnych parametrów specyficznych dla silnika:
Kod
rf_param
regularization_factor()Wreszcie, niektóre parametry dostrajania są związane z transformacjami. Dobrym przykładem jest parametr kary związany z wieloma modelami regresji regularyzowanej. Ten parametr jest nieujemny i często przedstawia się go w skali logarytmicznej. Podstawowy obiekt parametru dials wskazuje, że domyślnie używana jest transformacja:
Kod
penalty()Jest to ważna informacja, zwłaszcza przy zmianie zakresu. Nowe wartości zakresu muszą być w przekształconych jednostkach:
Kod
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.1001 0.1805 0.3115 0.3905 0.5582 0.9919 Min. 1st Qu. Median Mean 3rd Qu. Max.
1.260 2.126 3.454 4.132 5.812 9.905 Skala może być zmieniona w razie potrzeby za pomocą argumentu trans.
Kod
penalty(trans = NULL, range = 10^c(-10, 0))